题目内容
某旅馆有客房120间,每间房的日租金为160元,每天都客满.旅馆装修后要提高租金,经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?比装修前日租金的总收入增加多少元?
考点:二次函数的应用
专题:
分析:首先设每间客房的日租金提高10x元,则每天客房出租数会减少6x间,进而表示出出租的房间数以及每间客房的利润,进而得出y与x的函数关系,即可得出答案.
解答:解:设每间客房的日租金提高10x元,则每天客房出租数会减少6x间.设装修后客房日租金总收入为y,
则y=(160+10x)(120-6x),
即y=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
当x=2时,ymax=19 440.
这时每间客房的日租金为160+10×2=180(元).
装修后比装修前日租金总收入增加19 440-120×160=240(元).
答:每间客房的日租金提高到180元时,客房日租金的总收入最高;装修后比装修前日租金总收入增加240元.
则y=(160+10x)(120-6x),
即y=-60(x-2)2+19440.
∵x≥0,且120-6x>0,
∴0≤x<20.
当x=2时,ymax=19 440.
这时每间客房的日租金为160+10×2=180(元).
装修后比装修前日租金总收入增加19 440-120×160=240(元).
答:每间客房的日租金提高到180元时,客房日租金的总收入最高;装修后比装修前日租金总收入增加240元.
点评:此题主要考查了二次函数的应用,得出y与x的函数关系是解题关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
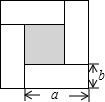 如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )
如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为( )| A、a2-b2=(a+b)(a-b) |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=(a+b)2-4ab |
| D、a2+ab=a(a+b) |
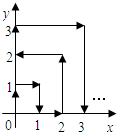 如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )
如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )| A、(0,9) |
| B、(9,0) |
| C、(0,8) |
| D、( 8,0) |
观察下列图形:

请用你发现的规律直接求出图④中的数y和图⑤中的数x,则x+y=( )

请用你发现的规律直接求出图④中的数y和图⑤中的数x,则x+y=( )
| A、10 | B、-14 | C、-12 | D、6 |

 如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.
如图,用一段长为30m的篱笆围出一个一边靠墙的矩形菜园,墙长为18m.设矩形的一边长为xm,面积为ym2.