题目内容
16.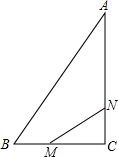 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点M以每秒1cm的速度从点B向点C移动;同时动点N以3cm的速度从点C向A移动,当点N到达点A时,两点都停止移动,连接MN,设移动时间为t秒.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点M以每秒1cm的速度从点B向点C移动;同时动点N以3cm的速度从点C向A移动,当点N到达点A时,两点都停止移动,连接MN,设移动时间为t秒.(1)当t为何值时,S△MNC=S四边形ABMN?
(2)当t为何值时,△MNC与△ABC相似?
分析 (1)由题意可知:CM=6-t,CN=3t,因为S△MNC=S四边形ABMN,所以S△MNC是△ABC的面积一半,由此列出方程解答即可;
(2)分两种情况:△MCN∽△ACB,△MCN∽△BCA,得出对应线段的比计算得出答案即可.
解答 解:(1)∵AC=8cm,BC=6cm,
∴S△ABC=24cm2,
∵CM=6-t,CN=3t,S△MNC=S四边形ABMN,
∴$\frac{1}{2}$×3t(6-t)=12,
解得:t1=2,t2=4;
∵当点N到达点A时,两点都停止移动,
∴0<t<$\frac{8}{3}$,
∴当t=2时,S△MNC=S四边形ABMN.
(2)①当△MCN∽△ACB时,
则$\frac{MC}{AC}$=$\frac{CN}{CB}$,
即$\frac{6-t}{8}$=$\frac{3t}{6}$,
解得:t=$\frac{6}{5}$;
②当△MCN∽△BCA时,
则$\frac{MC}{CB}$=$\frac{CN}{AC}$,
即$\frac{6-t}{6}$=$\frac{3t}{8}$,
解得:t=$\frac{24}{13}$,
答:当t为$\frac{6}{5}$,或$\frac{24}{13}$时,△MNC与△ABC相似.
点评 此题考查一元二次方程的实际运用,相似的性质,掌握三角形的面积和分类探讨是解决问题的关键.

练习册系列答案
相关题目
4.下列函数中,y的值随x值的增大而减小的是( )
①y=8x-1;②y=-0.6x;③y=$\sqrt{5}$x+1;④y=($\sqrt{2}$-$\frac{3}{2}$)x.
①y=8x-1;②y=-0.6x;③y=$\sqrt{5}$x+1;④y=($\sqrt{2}$-$\frac{3}{2}$)x.
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
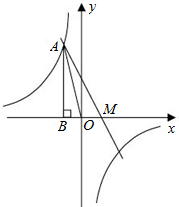 如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).
如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).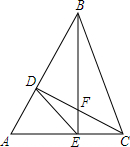 如图,△ABC中,∠A=60°,△ABC高BE、CD交于点F,下列说法中:①AD•AB=AE•AC,②BF•EF=CF•DF,③S△ABC=4S△AED,④BC=2DE,其中正确的有( )
如图,△ABC中,∠A=60°,△ABC高BE、CD交于点F,下列说法中:①AD•AB=AE•AC,②BF•EF=CF•DF,③S△ABC=4S△AED,④BC=2DE,其中正确的有( ) 如图,某工厂的工人师傅在一长方形铁板中挖掉一个半径为acm的圆,用代数式表示剩余部分的面积(2ab-πa2)cm2.
如图,某工厂的工人师傅在一长方形铁板中挖掉一个半径为acm的圆,用代数式表示剩余部分的面积(2ab-πa2)cm2.