题目内容
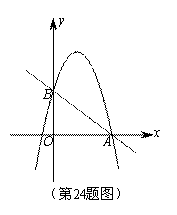
如图,已知二次函数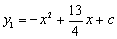 的图象与
的图象与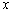 轴的一个交点为A(4,0),与
轴的一个交点为A(4,0),与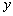 轴的交点为B,过A、B的直线为
轴的交点为B,过A、B的直线为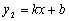 。
。
(1)求二次函数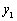 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足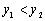 的自变量
的自变量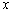 的取值范围;
的取值范围;
(3)在两坐标轴上是否存在点P,使得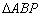 是以AB为底边的等腰三角形?若存在,
是以AB为底边的等腰三角形?若存在,
求出P点的坐标;若不存在,请说明理由。
解:
(1)将A(4,0)代入 得:
得:
 ,解得:
,解得: 。
。
∴所求二次函数 的解析式为:
的解析式为: …………………2分
…………………2分
当 时,故点B的坐标为:B(0,3) ………………………………4分
时,故点B的坐标为:B(0,3) ………………………………4分
(2)满足 的自变量x的取值范围是:
的自变量x的取值范围是: 或
或 ………………8分
………………8分
(3)存在。
如图,作线段AB的垂直平分线l,垂足为C,分别交x轴和y于 和
和 ,
,
 ∵A(4,0),B(0,3)
∵A(4,0),B(0,3)
∴OA=4,OB=3
∴在Rt AOB中,
AOB中,
∴
∵Rt ACP1和Rt
ACP1和Rt AOB有公共角∠OAB
AOB有公共角∠OAB
∴Rt ACP1∽Rt
ACP1∽Rt AOB
AOB
∴ ,即:
,即: ,解得:
,解得:
而
∴点 的坐标为:
的坐标为: (
( ,0) …………………………………………10分
,0) …………………………………………10分
∵Rt P2CB和Rt
P2CB和Rt AOB有公共角∠OBA
AOB有公共角∠OBA
∴Rt P2CB∽Rt
P2CB∽Rt AOB
AOB
∴ ,即:
,即: ,解得:
,解得:
而
∴点 的坐标为:
的坐标为: (0,
(0, )
)
∴点P的坐标为: (
( ,0),
,0), (0,
(0, ) ……………………12分
) ……………………12分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 ,电视正在播放新闻联播
,电视正在播放新闻联播 0°,AC=BC=AD.
0°,AC=BC=AD. ∠A的平分线交CD于E;
∠A的平分线交CD于E;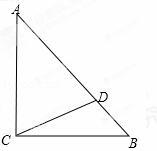
 ,其中
,其中 是方程
是方程 的根。
的根。

 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.