题目内容
17．
如图，⊙O的半径为1，弦AB=$\sqrt{2}$，则圆周角∠ACB=135°．
分析 延长AO交⊙O于D，连接DB，由圆周角定理得到∠ABD=90°，求得sin∠D=$\frac{AB}{AD}$=$\frac{\sqrt{2}}{2}$，得到∠D=45°，根据圆内接四边形的性质即可得到结论．
解答 
解：延长AO交⊙O于D，连接DB，
∴∠ABD=90°，
∵⊙O的半径为1，弦AB=$\sqrt{2}$，
∴AD=2，
∴sin∠D=$\frac{AB}{AD}$=$\frac{\sqrt{2}}{2}$，
∴∠D=45°，
∴∠ACB=135°．
故答案为：135°
点评 本题考查了圆周角定理，圆内接四边形的性质，正确的作出辅助线是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知直线a，b，点P是a，b外的任意一点，过点P分别画a，b的垂线．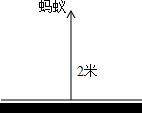
如图，蚂蚁在距巢穴2米远找到一只苍蝇，决定将其搬回家，可蚂蚁每一分钟内前进1米，却被风刮退2米，请问这只蚂蚁能否回到巢穴？如不能，请说明理由；如能，算一算何时能回巢穴．
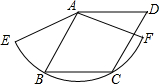如图，已知菱形ABCD的边长为3 cm，B，C两点在扇形AEF的$\widehat{EF}$上，求$\widehat{BC}$的长度及扇形ABC的面积．
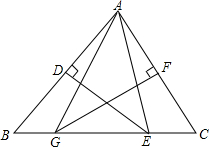如图，△ABC中，BC=12，∠BAC=70°，AB的垂直平分线交BC边于点E，AC的垂直平分线交BC边于点G．能否求出∠EAG的度数和△AEG的周长？
如图为一个正方体的展开图，图中已标出三个面在正方体中的位置f表示前面，r表示右面，d表示下面．试判定另外三个面a、b、c在正方体中的位置．