题目内容
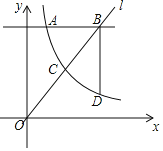
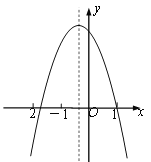
【题目】已知二次函数y＝ax2＋bx＋c的图像如图所示，则下列结论正确的个数有（ ）
①c＞0；②b2－4ac＜0；③ a－b＋c＞0；④当x＞－1时，y随x的增大而减小．
A.4个B.3个C.2个D.1个
【答案】C
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据抛物线与x轴交点及x=-1时二次函数的值的情况进行推理，进而对所得结论进行判断．
解：由图象可知，a＜0，c＞0，故①正确；抛物线与x轴有两个交点，则b-4ac>0,故②错误;∵当x=-1时，y>0,即a-b+c>0， 故③正确;
由图象可知，图象开口向下，对称轴x＞-1，在对称轴右侧， y随x的增大而减小，而在对称轴左侧和-1之间，是y随x的增大而减小，故④错误．
故选：C．
练习册系列答案
相关题目
【题目】在二次函数的学习中，教材有如下内容：
例1 函数图象求一元二次方程
的近似解（精确到0.1）．
解：设有二次函数
，列表并作出它的图象（图1）．
| … |
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
| … |
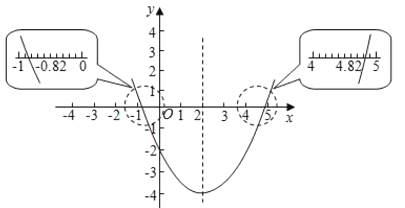
观察抛物线和
轴交点的位置，估计出交点的横坐标分别约为
和4.8，所以得出方程精确到0.1的近似解为
，
，利用二次函数
的图象求出一元二次方程
的解的方法称为图象法，这种方法常用来求方程的近似解．
小聪和小明通过例题的学习，体会到利用函数图象可以求出方程的近似解．于是他们尝试利用图象法探宄方程
的近似解，做法如下：
小聪的做法：令函数
，列表并画出函数的图象，借助图象得到方程的近似解．
小明的做法：因为
，所以先将方程的两边同时除以，变形得到方程
，再令函数
和
，列表并画出这两个函数的图象，借助图象得到方程的近似解．
请你选择小聪或小明的做法，求出方程的近似解（精确到0.1）．