题目内容
19.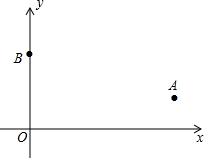 如图,在平面直角坐标系中,点A(5,1)和点B(0,3)是第一象限内的两点.
如图,在平面直角坐标系中,点A(5,1)和点B(0,3)是第一象限内的两点.(1)请在x轴上作出一点P,使PA+PB的最小值,并求出这个最小值;
(2)求直线PB的函数关系式;
(3)若(2)中的一次函数图象为直线m,求直线m沿y轴如何平移可使平移后的直线过点A.
分析 (1)作点A关于x轴的对称点A′,连接A′B交x轴于点P,则A′B的长即为PA+PB的最小值,利用两点间的距离公式求出A′B的长即可;
(2)利用待定系数法求出直线A′B的解析式即可;
(3)利用待定系数法求出直线平移后的解析式,再求直线与x轴的交点即可得出结论.
解答  解:(1)如图,作点A关于x轴的对称点A′,连接A′B交x轴于点,
解:(1)如图,作点A关于x轴的对称点A′,连接A′B交x轴于点,
∵A(5,1),
∴A′(5,-1).
∵B(0,3),
∴A′B=$\sqrt{{5}^{2}+(-1-3)^{2}}$=$\sqrt{25+16}$=$\sqrt{41}$,
∴PA+PB的最小值是$\sqrt{41}$;
(2)设直线PB的解析式为y=kx+b(k≠0),
∵A′(5,-1),B(0,3),
∴$\left\{\begin{array}{l}5k+b=-1\\ b=3\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{4}{5}\\ b=3\end{array}\right.$,
∴直线PB的解析式为:y=-$\frac{4}{5}$x+3;
(3)设平移后的解析式为y=-$\frac{4}{5}$x+m,
∵A(5,1)
∴-$\frac{4}{5}$×5+m=1,解得m=5,
∴平移后的解析式为y=-$\frac{4}{5}$x+5,
∴直线与y轴的交点为:(0,5).
∵5-3=2,
∴直线m沿y轴向上平移2个单位过点A.
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点、利用待定系数法求一次函数的解析式、轴对称-最短路线问题等知识,在解答(1)时要作出辅助线,利用数形结合求解.

练习册系列答案
相关题目
10.上网费包括网络使用费(每月38元)和上网通讯费(每小时2元),某电信局对拨号上网用户实行优惠,具体优惠政策如下:
(1)若小明家四月份上网28小时,应缴上网费多少?
(2)若小明家五月份上网80小时,应缴上网费多少元?
(3)如果用x表示每月的上网时间,y表示上网费用,你能用代数式分别表示出各时间段的上网费用吗?
| 上网时间 | 优惠标准 |
| 0~30小时(不超过30) | 无优惠 |
| 30~50小时(不超过50) | 通讯费优惠30% |
| 50~100小时(不超过100) | 通讯费优惠40% |
| 100小时以上 | 通讯费优惠50% |
(2)若小明家五月份上网80小时,应缴上网费多少元?
(3)如果用x表示每月的上网时间,y表示上网费用,你能用代数式分别表示出各时间段的上网费用吗?
11.有下列四个命题,其中正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 三点确定一个圆 | |
| C. | 三角形的内心到三角形三个顶点的距离相等 | |
| D. | 相等的弧所对的圆心角相等 |
20.若A(1,y1),B(-1,y2),C(4,y3)在抛物线上y=-(x-2)2+m上,则( )
| A. | y3>y2>y1 | B. | y1>y3>y2 | C. | y1>y2>y3 | D. | y3>y2>y1 |
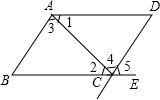 如图.在图中,
如图.在图中,