题目内容
阅读下面材料:
小辉遇到这样一个问题:如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E在边BC上,∠DAE=45°.若BD=3,CE=1,求DE的长.
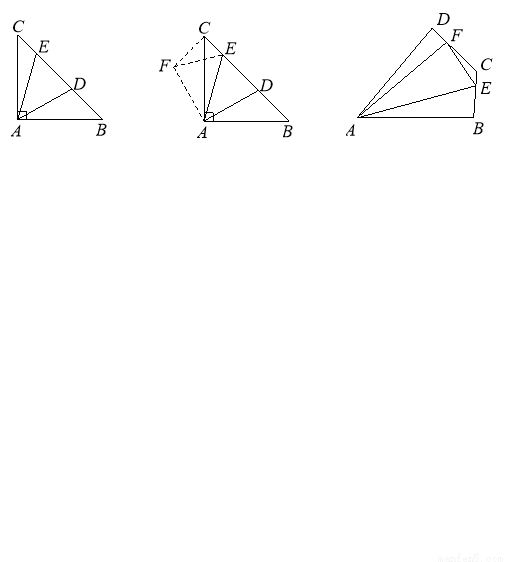
小辉发现,将△ABD绕点A按逆时针方向旋转90º,得到△ACF,连接EF(如图2),由图形旋转的性质和等腰直角三角形的性质以及∠DAE=45°,可证△FAE≌△DAE,得FE=DE.解△FCE,可求得FE(即DE)的长.
请回答:在图2中,∠FCE的度数是 ,DE的长为 .
参考小辉思考问题的方法,解决问题:
如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是边BC,CD上的点,且∠EAF=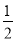 ∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
90°; ;EF=BE+FD
;EF=BE+FD
【解析】
试题分析:(1)根据旋转图形可得∠FCA=∠B=45°,则∠FCE=90°,CF=BD=3,CE=1,根据△FCE的勾股定理求出EF的长度,即ED=EF;(2)将图形旋转可得DG=BE,AE=AG,∠DAG=∠BAE,∠B=∠ADG,根据(1)的方法证明△AEF和△AGF全等,得到EF=FG,根据FG=DG+FD,说明EF=BE+FD.
试题解析:90°; .
.
猜想:EF=BE+FD;

理由如下:如图,将△ABE绕点A按逆时针方向旋转,使AB与AD重合,得到△ADG,
∴BE=DG,AE=AG,∠DAG=∠BAE,∠B=∠ADG,∵∠B+∠ADC=180°,∠B=∠ADG,
∴∠ADG+∠ADC=180°,即点F,D,G在同一条直线上.∵∠EAF= ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
即∠GAF=∠EAF. 在△AEF和△AGF中,
∴△AEF≌△AGF, ∴EF=FG. ∵FG=DG+FD=BE+DF, ∴EF=BE+FD.
考点:旋转图形的性质、三角形全等的判定.

 阶梯计算系列答案
阶梯计算系列答案 ABCD中,延长BC到E,使CE:BC=1:2,连接AE交DC于F,求
ABCD中,延长BC到E,使CE:BC=1:2,连接AE交DC于F,求 :
: =
= 
 B.
B.  C.
C. D.
D.
 的常数项是0,则m的值是( ).
的常数项是0,则m的值是( ).
 的长.
的长. 的图象在其每一分支上,y随x的增大而减小,则此反比例函数的解析式可以是 .(注:只需写出一个正确答案即可)
的图象在其每一分支上,y随x的增大而减小,则此反比例函数的解析式可以是 .(注:只需写出一个正确答案即可) ,则阴影部分图形的面积为_________(用含有π的代数式表示).
,则阴影部分图形的面积为_________(用含有π的代数式表示).
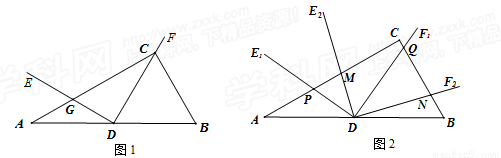
 (
(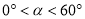 ),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求
),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求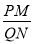 的值;
的值;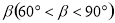 ,(2)中的其余条件不变,判断
,(2)中的其余条件不变,判断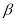 的式子表示);如果不是,请说明理由.
的式子表示);如果不是,请说明理由.