题目内容
如图,在半径为6cm的⊙O中,圆心O到弦AB的距离OE为3cm.

(1)求弦AB的长;(2)求劣弧 的长.
的长.
(1)AB= ;(2)
;(2) .
.
【解析】
试题分析:(1)根据勾股定理求出AE的长度,根据垂径定理可得AB=2AE;(2)根据锐角三角函数求出∠AOE的度数,然后得出∠AOB的度数,根据弧长的计算公式求出弧长.
试题解析:(1)∵AB为⊙O的弦,OE⊥AB于E,∴AE=BE= AB.
AB.
在Rt△AOE中,OA=6,OE=3, ∴AE= =
= =
= =
= ,
,
∴AB=2AE= .
.
(2)由(1)知,在Rt△AOE中,∠AEO=90°,OA=6,OE=3,∴cos∠AOE= =
= ,
,
∴∠AOE=60°,∴∠AOB=2∠AOE=120°,
∴ 的长
的长 =
= =
= .
.
考点:垂径定理、弧长计算公式、三角函数的应用.

练习册系列答案
相关题目
甲、乙、丙、丁四位选手各射击10次,每人的平均成绩是9.3环,方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(环) | 0.035 | 0.016 | 0.022 | 0.025 |
则这四人中成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁
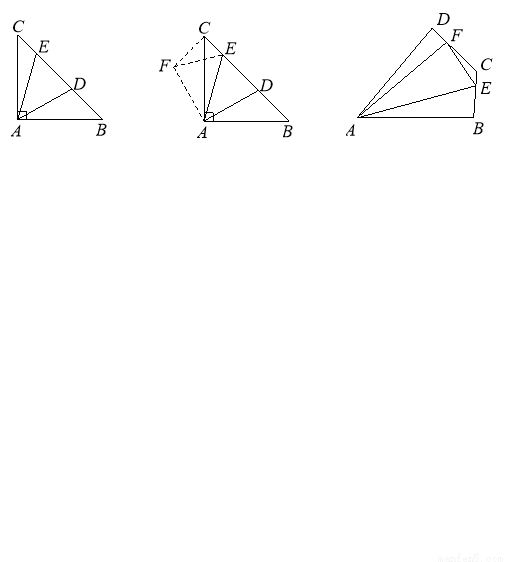
 ∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由. 的图象上有点P1,P2,P3,…,Pn,Pn+1,它们的横坐标依次为1,2,3,…,n,n+1.过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为
的图象上有点P1,P2,P3,…,Pn,Pn+1,它们的横坐标依次为1,2,3,…,n,n+1.过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为 ,
, ,
, ,…,
,…, ,则点P1的坐标为 ;
,则点P1的坐标为 ; = ;
= ; = .(用含n的代数式表示)
= .(用含n的代数式表示)

