题目内容
如图1,在Rt△ABC中,∠ACB=90°,∠B=60°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.
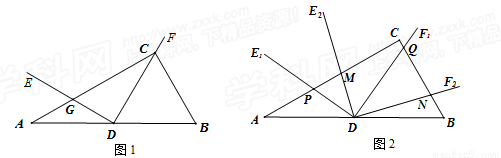
(1)求∠ADE的度数;
(2)如图2,将图1中的∠EDF绕点D顺时针方向旋转角 (
( ),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求
),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2 , DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求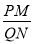 的值;
的值;
(3)若图1中∠B=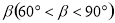 ,(2)中的其余条件不变,判断
,(2)中的其余条件不变,判断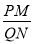 的值是否为定值,如果是,请直接写出这个值(用含
的值是否为定值,如果是,请直接写出这个值(用含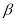 的式子表示);如果不是,请说明理由.
的式子表示);如果不是,请说明理由.
(1)30°;(2) ;(3)是定值,值为
;(3)是定值,值为 .
.
【解析】
试题分析:(1)由D为AB的中点,得到CD=DB,∠DCB=∠B,进一步得到∠DCB=∠B=∠CDB=60°,可以求得∠ADE=30°;
(2)先证△PMD∽△QND,过点D分别做DG⊥AC于G, DH⊥BC于H,可得 ,再证四边形CGDH 为矩形,得到CG=DH=AG,故有
,再证四边形CGDH 为矩形,得到CG=DH=AG,故有 ,即
,即 ;
;
(3)是定值,值为 .
.
试题解析:(1)∵∠ACB=90°,D为AB的中点,∴CD=DB,∴∠DCB=∠B,∵∠B=60°,∴∠DCB=∠B=∠CDB=60°,∴∠CDA=120°,∵ ∠EDC=90°,∴∠ADE=30°;
∠EDC=90°,∴∠ADE=30°;

(2)∵∠C=90°,∠MDN=90°,∴∠DMC+∠CND=180°,∵∠DMC+∠PMD=180°,∴∠CND=∠PMD,同理∠CPD=∠DQN,∴△PMD∽△QND,过点D分别做DG⊥AC于G, DH⊥BC于H,可知DG, DH分别为△PMD和△QND的高,∴ ,∵DG⊥AC于G, DH⊥BC于H,∴DG ∥BC,∵D为AC中点,∴G为AC中点,∵∠C=90°,∴四边形CGDH 为矩形有CG=DH=AG,Rt△AGD中,
,∵DG⊥AC于G, DH⊥BC于H,∴DG ∥BC,∵D为AC中点,∴G为AC中点,∵∠C=90°,∴四边形CGDH 为矩形有CG=DH=AG,Rt△AGD中, ,即
,即 ;
;

(3)是定值,值为 .
.
考点:相似三角形综合题.

 小学教材完全解读系列答案
小学教材完全解读系列答案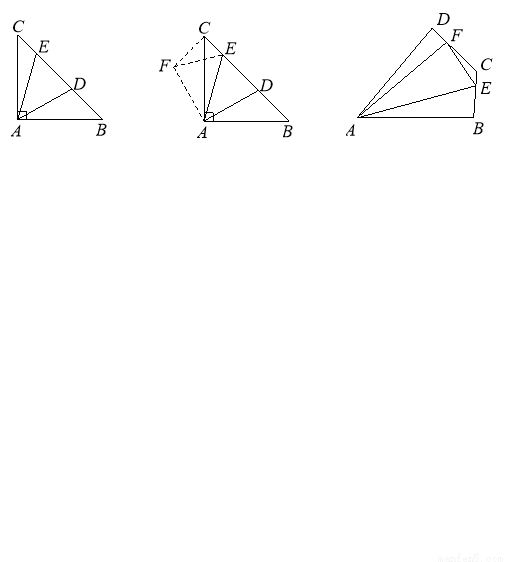
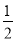 ∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由.
∠BAD.猜想线段BE,EF,FD之间的数量关系并说明理由. B.
B. C.
C. D.
D.

 ,则
,则 的值为( )
的值为( )  B.
B. C.
C. D.
D.

 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°,菱形An﹣1BnAnCn的周长为 .

