题目内容
10．若关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x+y=a}\\{x+2y=a-3}\end{array}\right.$的解满足x+y＜1，则a的取值范围为a＜3．分析 方程组两方程相加表示出x+y，代入不等式求出a的范围即可．
解答 解：$\left\{\begin{array}{l}{2x+y=a①}\\{x+2y=a-3②}\end{array}\right.$，
①+②得：3（x+y）=2a-3，即x+y=$\frac{2a-3}{3}$，
代入不等式得：$\frac{2a-3}{3}$＜1，
解得：a＜3．
故答案为：a＜3．
点评 此题考查了二元一次方程组的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
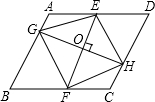如图，点O是?ABCD的对称中心，过点O作两条互相垂直的直线EF，GH，分别与?ABCD的四条边交于点E，F和点G，H，试说明四边形EGFH是中心对称图形，它有几条对称轴．
2．6的相反数是（ ）
| A． | 6 | B． | -6 | C． | $\frac{1}{6}$ | D． | -$\frac{1}{6}$ |
某公司推销一种产品，公司付给推销员的月报酬有两种方案如图所示：其中方案一所示图形是顶点B在原点的抛物线的一部分，方案二所示图形是射线．设推销员推销产品的数量为x（件），付给推销员的月报酬为y（元）．