题目内容
15.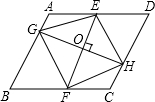 如图,点O是?ABCD的对称中心,过点O作两条互相垂直的直线EF,GH,分别与?ABCD的四条边交于点E,F和点G,H,试说明四边形EGFH是中心对称图形,它有几条对称轴.
如图,点O是?ABCD的对称中心,过点O作两条互相垂直的直线EF,GH,分别与?ABCD的四条边交于点E,F和点G,H,试说明四边形EGFH是中心对称图形,它有几条对称轴.
分析 根据对角线互相垂直的平行四边形是菱形.由已知条件证明OE=OF,同理OG=OH,所以四边形EGFH是平行四边形,又因为EF⊥GH,所以四边形EGFH是菱形,进而得出答案.
解答 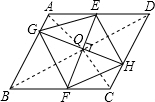 解:四边形EGFH是中心对称图形,它有2条对称轴.
解:四边形EGFH是中心对称图形,它有2条对称轴.
理由:连接AC,BD,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD∥BC,
∴∠ADB=∠DBC,
在△EOD和△FOB中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{DO=BO}\\{∠DOE=∠BOF}\end{array}\right.$,
∴△EOD≌△FOB(ASA),
∴EO=FO,
同理可得:GO=HO,
又∵EF⊥GH,
∴四边形EGFH是菱形,
∴四边形EGFH是中心对称图形,它有2条对称轴.
点评 此题主要考查了菱形的判定以及全等三角形的判定与性质,ASA得出△EOD≌△FOB是解题关键.

练习册系列答案
相关题目
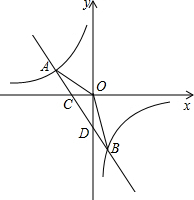 一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C.已知点A(-2,1),点B的坐标为(1,m).