题目内容
20.先阅读下列知识,然后回答后面的问题:(1)二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解的情况有以下三种:
当$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$=$\frac{{c}_{1}}{{c}_{2}}$时,方程组有无数解.
当$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$≠$\frac{{c}_{1}}{{c}_{2}}$时,方程组有无解.
当$\frac{{a}_{1}}{{a}_{2}}$≠$\frac{{b}_{1}}{{b}_{2}}$时,方程组有唯一解.
(2)判断二元一次方程组$\left\{\begin{array}{l}{x+y=2}\\{2x+2y=4}\end{array}\right.$的解的情况:无数解.
判断二元一次方程组$\left\{\begin{array}{l}{2x-y=1}\\{4x-2y=3}\end{array}\right.$的解的情况:无解.
判断二元一次方程组$\left\{\begin{array}{l}{2x+y=1}\\{4x-2y=3}\end{array}\right.$的解的情况:唯一解.
(3)小明在解下面的二元一次方程组时,碰到了一个非常“严重”的问题,发现“10=8”,他知道这是不可能的,但是又找不到错误的原因,请你解释一下:
解方程组:$\left\{\begin{array}{l}{2x+y=5①}\\{4x+2y=8②}\end{array}\right.$.
解:由①得y=5-2x,代入②得4x+2(5-2x)=8,得10=8.
请指出出现这种错误的原因.
分析 (1)根据二元一次方程组的解与系数的关系求解即可;
(2)根据(1)的结论求解即可;
(3)根据(1)的结论可知,原方程组外角,所以出现错误.
解答 解:(1)二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解的情况有以下三种:
当$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$=$\frac{{c}_{1}}{{c}_{2}}$时,方程组有无数解.
当$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$≠$\frac{{c}_{1}}{{c}_{2}}$时,方程组有无解.
当$\frac{{a}_{1}}{{a}_{2}}$≠$\frac{{b}_{1}}{{b}_{2}}$时,方程组有唯一解.
故答案为无数;无;唯一;
(2)∵$\frac{1}{2}$=$\frac{1}{2}$=$\frac{2}{4}$,
∴二元一次方程组$\left\{\begin{array}{l}{x+y=2}\\{2x+2y=4}\end{array}\right.$有无数解;
∵$\frac{2}{4}$=$\frac{-1}{-2}$≠$\frac{1}{3}$,
∴二元一次方程组$\left\{\begin{array}{l}{2x-y=1}\\{4x-2y=3}\end{array}\right.$无解;
∵$\frac{2}{4}$≠$\frac{1}{-2}$,
∴二元一次方程组$\left\{\begin{array}{l}{2x+y=1}\\{4x-2y=3}\end{array}\right.$有唯一解;
故答案为无数解;无解;唯一解;
(3)∵$\frac{2}{4}$=$\frac{1}{2}$≠$\frac{5}{8}$,
∴二元一次方程组$\left\{\begin{array}{l}{2x+y=5①}\\{4x+2y=8②}\end{array}\right.$无解,
小明出现了10=8的这种错误.
点评 本题考查了二元一次方程组的解的定义:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.掌握二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解的三种情况是解题的关键.

| A. | 4 | B. | 8 | C. | ±2 | D. | ±4 |
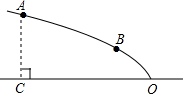 如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.
如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米. 如图所示,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=150°.
如图所示,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=150°.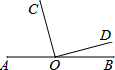 如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.
如图,点O是直线AB上一点,OC⊥OD,∠AOC:∠BOD=5:1,那么∠AOC的度数是75°.