题目内容
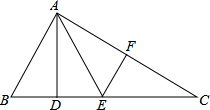 如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,若△ABC周长13,AC=6,DC=
如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,若△ABC周长13,AC=6,DC=考点:线段垂直平分线的性质,等腰三角形的判定与性质
专题:
分析:根据线段垂直平分线上的点到两端点的距离相等可得AE=EC,根据等腰三角形的性质可得AB=AE,然后求出DC=
(AB+BC),再根据三角形的周长和AC的长度求解即可.
| 1 |
| 2 |
解答:解:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴DC=DE+EC=
(AB+BC),
∵△ABC周长13,AC=6,
∴AB+BC=13-6=7,
∴DC=
×7=3.5.
故答案为:3.5.
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴DC=DE+EC=
| 1 |
| 2 |
∵△ABC周长13,AC=6,
∴AB+BC=13-6=7,
∴DC=
| 1 |
| 2 |
故答案为:3.5.
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等腰三角形的性质,熟记各性质并求出DC=
(AB+BC)是解题的关键.
| 1 |
| 2 |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 如图已知:在△ABC中,AB=AC,点D在BC边上,且BD=CD,求证:AD平分∠BAC.
如图已知:在△ABC中,AB=AC,点D在BC边上,且BD=CD,求证:AD平分∠BAC. 如图,BC⊥AC,DE⊥AC,点D是AB的中点,∠A=30°,DE=1.8.求AB的长.
如图,BC⊥AC,DE⊥AC,点D是AB的中点,∠A=30°,DE=1.8.求AB的长.