题目内容
19.如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:(1)在图1中画出一条长为$\sqrt{5}$的线段;(要求线段的端点都在格点上)
(2)在图2中画出一个以格点为顶点,面积为10的等腰三角形.(要求三角形的顶点都在格点上)
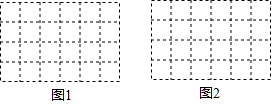
分析 (1)利用勾股定理的逆定理确定两直角边的长即可确定答案;
(2)根据三角形的面积公式确定三角形的底边长和高即可.
解答 解:如图所示:
点评 本题考查了等腰三角形的性质、勾股定理等知识,解题的关键是了解如何根据题意构造直角三角形并利用勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.抛物线y=2(x+1)2+1的顶点坐标是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
7.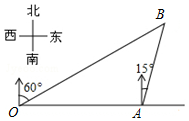 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )| A. | 3$\sqrt{2}$km | B. | 3$\sqrt{3}$km | C. | 4 km | D. | (3$\sqrt{3}$-3)km |
8.我市10月的某周七天的最高气温(单位:℃)统计如下:19,20,24,22,24,26,27,则这组数据的中位数与众数分别是( )
| A. | 23,24 | B. | 24,22 | C. | 22,24 | D. | 24,24 |
9. 如图,已知AE,BD是△ABC的角平分线,AE与BD相交于点P,若AB=BC,且AB≠AC,则图中的全等三角形有( )
如图,已知AE,BD是△ABC的角平分线,AE与BD相交于点P,若AB=BC,且AB≠AC,则图中的全等三角形有( )
 如图,已知AE,BD是△ABC的角平分线,AE与BD相交于点P,若AB=BC,且AB≠AC,则图中的全等三角形有( )
如图,已知AE,BD是△ABC的角平分线,AE与BD相交于点P,若AB=BC,且AB≠AC,则图中的全等三角形有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
 方程术是《九章算术》最高的数学成就,《九章算术》中“盈不足”一章中记载:“今有大器五小器一容三斛(古代的一种容量单位),大器一小器五容二斛,…”译文:“已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛,…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛.
方程术是《九章算术》最高的数学成就,《九章算术》中“盈不足”一章中记载:“今有大器五小器一容三斛(古代的一种容量单位),大器一小器五容二斛,…”译文:“已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛,…”则一个大桶和一个小桶一共可以盛酒$\frac{5}{6}$斛.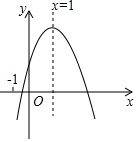 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列五个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列五个结论: