题目内容
(1)(3a)2
(2)(-3a)3
(3)a10÷a2
(4)m8÷m2•m3
(5)3xy2(2xy2-3xy)
(6)(x+5)(x-7)
(7)(2x+
)(2x-
)
(8)(x+3)2
(9)(x-3)2
(10)6x3y3÷2xy.
(2)(-3a)3
(3)a10÷a2
(4)m8÷m2•m3
(5)3xy2(2xy2-3xy)
(6)(x+5)(x-7)
(7)(2x+
| 1 |
| 2 |
| 1 |
| 2 |
(8)(x+3)2
(9)(x-3)2
(10)6x3y3÷2xy.
考点:整式的混合运算
专题:计算题
分析:(1)原式利用积的乘方运算法则计算即可得到结果;
(2)原式利用积的乘方运算法则计算即可得到结果;
(3)原式利用同底数幂的除法法则计算即可得到结果;
(4)原式利用同底数幂的除法法则计算即可得到结果;
(5)原式利用单项式乘多项式法则计算即可得到结果;
(6)原式利用多项式乘多项式法则计算即可得到结果;
(7)原式利用平方差公式计算即可得到结果;
(8)原式利用完全平方公式展开即可得到结果;
(9)原式利用完全平方公式展开即可得到结果;
(10)原式利用单项式除以单项式法则计算即可得到结果.
(2)原式利用积的乘方运算法则计算即可得到结果;
(3)原式利用同底数幂的除法法则计算即可得到结果;
(4)原式利用同底数幂的除法法则计算即可得到结果;
(5)原式利用单项式乘多项式法则计算即可得到结果;
(6)原式利用多项式乘多项式法则计算即可得到结果;
(7)原式利用平方差公式计算即可得到结果;
(8)原式利用完全平方公式展开即可得到结果;
(9)原式利用完全平方公式展开即可得到结果;
(10)原式利用单项式除以单项式法则计算即可得到结果.
解答:解:(1)(3a)2=9a2;
(2)(-3a)3=-27a3;
(3)a10÷a2=a8;
(4)m8÷m2•m3=m3;
(5)3xy2(2xy2-3xy)=6x2y4-9x2y3;
(6)(x+5)(x-7)=x2-2x-35;
(7)(2x+
)(2x-
)=4x2-
;
(8)(x+3)2=x2+6x+9;
(9)(x-3)2=x2-6x+9;
(10)6x3y3÷2xy=3x2y2.
(2)(-3a)3=-27a3;
(3)a10÷a2=a8;
(4)m8÷m2•m3=m3;
(5)3xy2(2xy2-3xy)=6x2y4-9x2y3;
(6)(x+5)(x-7)=x2-2x-35;
(7)(2x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(8)(x+3)2=x2+6x+9;
(9)(x-3)2=x2-6x+9;
(10)6x3y3÷2xy=3x2y2.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
| A、开口向下 |
| B、对称轴是x=-1 |
| C、顶点坐标是(1,2) |
| D、与x轴有两个交点 |
下列式子从左到右是因式分解的是( )
| A、(x+y)(x-y)=x2-y2 |
| B、x2-2x+3=x(x-2)+3 |
| C、a(x+y)=ax+ay |
| D、a2+2ab+b2=(a+b)2 |
在等边三角形,平行四边形,矩形,菱形,正方形,圆,正五边形,正六边形中,是中心对称图形但不是轴对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
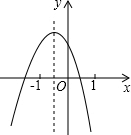 已知抛物线y=ax2+bx+c如图,则abc
已知抛物线y=ax2+bx+c如图,则abc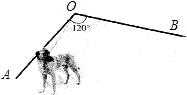 如图,墙OA、OB的夹角∠AOB=120°,一根3m长的绳子一端拴在墙角O处,另一端拴着一只小狗,求小狗可活动的区域的面积.(结果保留π)
如图,墙OA、OB的夹角∠AOB=120°,一根3m长的绳子一端拴在墙角O处,另一端拴着一只小狗,求小狗可活动的区域的面积.(结果保留π) 如图,在每个小正方形的边长均为1个单位长度的方格纸中,△ABO的顶点均与小正方形的顶点重合.以点O为坐标原点建立平面直角坐标系后,点A的坐标为(-2,4).
如图,在每个小正方形的边长均为1个单位长度的方格纸中,△ABO的顶点均与小正方形的顶点重合.以点O为坐标原点建立平面直角坐标系后,点A的坐标为(-2,4). 如图,已知BC=EF,∠ABC=∠DEF.
如图,已知BC=EF,∠ABC=∠DEF.