题目内容
14．
在一次为某位身患重病的小朋友募捐过程中，某年级有50师生通过微信平台奉献了爱心．小东对他们的捐款金额进行统计，并绘制了如下统计图．师生捐款金额的平均数和众数分别是（ ）| A． | 20，20 | B． | 32.4，30 | C． | 32.4，20 | D． | 20，30 |
分析 由统计图提供的信息，利用加权平均数的计算公式求出平均数，众数是这组数中出现次数最多的数，据此求解即可．
解答 解：由图可知，平均数是（6×10+13×20+20×30+8×50+3×100）÷50=32.4（元）．
捐款30元的有20人，人数最多，故众数是30元．
故选B．
点评 本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．除此之外，本题也考查了平均数与众数．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4．
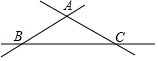如图，直线AB、BC、AC交于A、B、C三点，则图中内错角、同位角、同旁内角的对数分别是（ ）
如图，直线AB、BC、AC交于A、B、C三点，则图中内错角、同位角、同旁内角的对数分别是（ ）| A． | 6、12、6 | B． | 6、10、6 | C． | 4、12、4 | D． | 4、8、4 |
5．已知$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{3x+3y=m-1}\\{nx-y=4}\end{array}\right.$的解，则nm的值为（ ）
| A． | $\frac{1}{4}$ | B． | -$\frac{1}{4}$ | C． | 4 | D． | -4 |
2．算式（-2）×|-5|-|-3|之值为何（ ）
| A． | 13 | B． | 7 | C． | -13 | D． | -7 |
9．
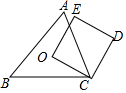如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述何者正确（ ）
如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述何者正确（ ）| A． | O是△AEB的外心，O是△AED的外心 | |
| B． | O是△AEB的外心，O不是△AED的外心 | |
| C． | O不是△AEB的外心，O是△AED的外心 | |
| D． | O不是△AEB的外心，O不是△AED的外心 |
19．在平面直角坐标系中，将点A（-1，3）向右平移2个单位长度，得到对应点B，则点B的坐标是（ ）
| A． | （-1，3） | B． | （1，3） | C． | （-3，3） | D． | （-1，5） |
6．
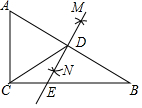如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于$\frac{1}{2}$AB） 为半径作弧，两弧相交于M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（ ）
如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于$\frac{1}{2}$AB） 为半径作弧，两弧相交于M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论错误的是（ ）| A． | ∠ADE=∠ACB | B． | ∠A=∠ADC | C． | ∠B=∠DCB | D． | ∠A=∠BED |
3．
如图是下面某个几何体的三种视图，则该几何体是（ ）
如图是下面某个几何体的三种视图，则该几何体是（ ）| A． | 圆锥 | B． | 圆柱 | C． | 三棱锥 | D． | 三棱柱 |
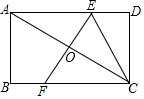如图，在矩形ABCD中，AB=3，∠BCA=30°，对角线AC的垂直平分线分别交AD，BC于点E、F，连接CE，则CE的长为2$\sqrt{3}$．