Question

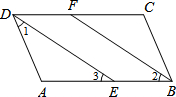
已知△ABC是等腰直角三角形，AB=AC，P为BC边中点．
（1）如图①，以P为顶点作∠MPN=45°，PM、PN分别交线段AB、AC于D、E两点，当AD=AE时，求证：△BPD≌△CPE；
（2）将①中的∠MPN绕点P旋转，PM、PN始终保持分别与线段AB、AC相交，如图②，试证明∠BDP+∠CEP的度数是个定值，且PD、PE分别平分∠BDE和∠CED．
（3）如图③，若以A为顶点作∠MAN=45°，边BC分别与AM、AN相交于点E、F，试证明：EF²=BE²+CF²．

Answer 1

考点：全等三角形的判定与性质,勾股定理的逆定理,等腰直角三角形

专题：

分析：（1）根据线段中点的定义可得BP=CP，再求出BD=CE，再根据等腰直角三角形的性质可得∠B=∠C=45°，然后利用“边角边”证明即可；
（2）求出∠BPD+∠CPE=135°，然后利用三角形的内角和定理列式计算即可求出∠BDP+∠CEP的度数；过点P作PF⊥AB于F，作PH⊥AC于H，然后求出△BPF和△CPH是全等的等腰直角三角形，然后求出PF=PH，把△PDF绕点P顺时针旋转，使PF与PH重合得到△PHK，根据旋转的性质可得PD=PK，∠DPF=∠KPH，再求出∠EPK=∠EPD=45°，然后利用“边角边”证明△DEP和△KEP全等，根据全等三角形对应角相等可得∠CEP=∠DEP，过点P作PG⊥DE于G，利用“角角边”证明△PEH和△PEG全等，根据全等三角形对应边相等可得PH=PG，从而得到PF=PG，再根据到角的两边距离相等的点在角的平分线上可得PD平分∠BDE；
（3）把△ABE绕点A逆时针旋转90°得到△ACD，根据旋转的性质可得AE=AD，BE=CD，∠ACD=∠B=45°，∠CAD=∠BAE，再求出△AEF和△ADF全等，根据全等三角形对应边相等可得EF=DF，再求出∠DCF=90°，然后利用勾股定理列式整理即可得证．

解答：（1）证明：∵P为BC边中点，
∴BP=CP，
∵AB=AC，AD=AE，
∴BD=CE，
∵△ABC是等腰直角三角形，AB=AC，
∴∠B=∠C=45°，
在△BPD和△CPE中，

BP=CP ∠B=∠C BD=CE

，
∴△BPD≌△CPE（SAS）；

（2）解：∵∠MPN=45°，
∴∠BPD+∠CPE=180°-45°=135°，
∵∠B=∠C=45°，
∴∠BDP+∠CEP=180°×2-45°×2-135°=135°，
即∠BDP+∠CEP的度数是定值135°；
过点P作PF⊥AB于F，作PH⊥AC于H，
易得△BPF≌△CPH，
所以，PF=PH，
把△PDF绕点P顺时针旋转，使PF与PH重合得到△PHK，
由旋转的性质得，PD=PK，∠DPF=∠KPH，
∵∠MPN=45°，
∴∠EPK=∠EPD=45°，
在△DEP和△KEP中，

PD=PK ∠EPK=∠EPD PE=PE

，
∴△DEP≌△KEP（SAS），
∴∠CEP=∠DEP，
∴PE平分∠CED，
过点P作PG⊥DE于G，
在△PEH和△PEG中，

∠CEP=∠DEP ∠PGE=∠PHE=90° PE=PE

，
∴△PEH≌△PEG（AAS），
∴PH=PG，
∵PF=PH，
∴PF=PG，
∴PD平分∠BDE；

（3）证明：把△ABE绕点A逆时针旋转90°得到△ACD，
由旋转的性质可得AE=AD，BE=CD，∠ACD=∠B=45°，∠CAD=∠BAE，
∵∠MAN=45°，
∴∠EAF=∠DAF=45°，
在△AEF和△ADF中，

AE=AD ∠EAF=∠DAF AF=AF

，
∴△AEF≌△ADF（SAS），
∵∠DCF=∠ACB+∠ACD=45°+45°=90°，
∴DF²=CD²+CF²，
∴EF²=BE²+CF²．

点评：本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，到角的两边距离相等的点在角的平分线上的性质，难点在于（2）作辅助线构造出全等三角形．