题目内容
15. 如图,点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=$\frac{1}{2}$A1M,△A1C1B的面积记为S1,则S1=$\frac{1}{4}$.
如图,点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=$\frac{1}{2}$A1M,△A1C1B的面积记为S1,则S1=$\frac{1}{4}$.
分析 根据点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,即可得出${S}_{△{A}_{1}BM}$=$\frac{1}{2}$OB×MB=$\frac{1}{2}$,再利用C1到BM的距离为A1到BM的距离的一半,得出S1=${S}_{△BM{C}_{1}}$=$\frac{1}{2}$${S}_{△{A}_{1}BM}$=$\frac{1}{4}$.
解答 解:过点M作MD⊥y轴于点D,过点A1作A1E⊥BM于点E,过点C1作C1F⊥BM于点F,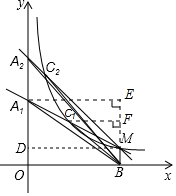
∵点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,
∴OB×BM=1,
∴${S}_{△{A}_{1}BM}$=$\frac{1}{2}$OB×MB=$\frac{1}{2}$,
∵A1C1=$\frac{1}{2}$A1M,即C1为A1M中点,
∴C1到BM的距离C1F为A1到BM的距离A1E的一半,
∴S1=${S}_{△BM{C}_{1}}$=$\frac{1}{2}$${S}_{△{A}_{1}BM}$=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 此题主要考查了反比例函数的综合应用以及三角形面积关系,根据同底三角形对应高的关系得出面积关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.若点P(a,1-a)在第一象限,则a的取值范围是( )
| A. | a<0 | B. | a<1 | C. | a>1 | D. | 0<a<1 |
 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.试说明:AD平分∠BAC.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.试说明:AD平分∠BAC. 将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F. 已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试证明:△ADM∽△MCP.
已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试证明:△ADM∽△MCP.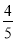 ,求BF的长.
,求BF的长.