题目内容
3. 将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)求证:CF∥AB
(2)求∠DFC的度数.
分析 (1)根据角平分线的定义求得∠FCE的度数,根据平行线的判定定理即可证得;
(2)在△CEF中,利用三角形的外角的性质定理,即可求解.
解答 (1)证明:由题意知,△ACB是等腰直角三角形,且∠ACB=∠DCB=90°,
∴∠B=45°.
∵CF平分∠DCE,
∴∠DCF=∠ECF=45°,
∴∠B=∠ECF,
∴CF∥AB.
(2)由三角板知,∠E=60°,
由(1)知,∠ECF=45°,
∵∠DFC=∠ECF+∠E,
∴∠DFC=45°+60°=105°.
点评 本题考查了直角三角形的性质,以及平行线的判定定理的综合运用,正确理解直角三角形的性质定理是关键.

练习册系列答案
相关题目
14.已知a<b,则下列不等式正确的是( )
| A. | 3a>3b | B. | a-3>b-3 | C. | -3a>-3b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
11.近似数0.360精确到的数位是( )
| A. | 十分位 | B. | 百分位 | C. | 千分位 | D. | 万分位 |
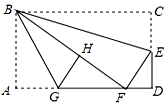 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°; ②AB:DE=AG:DF;
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°; ②AB:DE=AG:DF; 如图,点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=$\frac{1}{2}$A1M,△A1C1B的面积记为S1,则S1=$\frac{1}{4}$.
如图,点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=$\frac{1}{2}$A1M,△A1C1B的面积记为S1,则S1=$\frac{1}{4}$.