题目内容
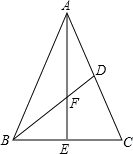
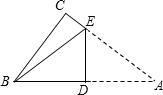
如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC=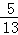 ,AB=13.
,AB=13.
(1)求AE的长;
(2)求tan∠DBC的值.
【考点】解直角三角形;勾股定理.
【分析】(1)根据AE⊥BC,垂足为点E,交BD于F,cos∠ABC=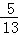 ,AB=13,可以求得BE的长,从而可以求得AE的长;
,AB=13,可以求得BE的长,从而可以求得AE的长;
(2)根据在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,可知AE、BD为△ABC的中线,从而可以利用重心定理得到EF的长,由AE⊥BC,从而可以得到tan∠DBC的值.
【解答】解:(1)∵AE⊥BC,
∴∠AEB=90°.
∵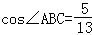 ,AB=13,
,AB=13,
∴BE=5.
∵在Rt△BEA中,BE2+AE2=AB2,
∴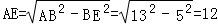 .
.
(2)∵AB=AC,AE⊥BC,
∴AE是BC边上的中线.
又∵BD是AC边上的中线,
∴F是△ABC的重心.
∵AE=12,
∴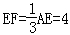 .
.
∵Rt△BEF中,BE=5,EF=4,
∴tan∠DBC=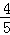 .
.
【点评】本题考查解直角三角形、勾股定理,解题的关键是明确直角三角形中边角的关系,知道重心定理.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 的一个有理化因式 .
的一个有理化因式 .

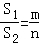 ,
, =
=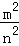 ,根据上述条件,判断S1+S3与S2+S4的大小关系,并说明理由.
,根据上述条件,判断S1+S3与S2+S4的大小关系,并说明理由.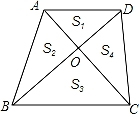
 是完成平方公式,那么k的值是
是完成平方公式,那么k的值是 B.
B. C.
C. D.
D.