题目内容
.如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是__________.
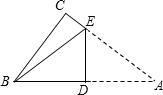
 .
.

【考点】翻折变换(折叠问题).
【分析】由翻折的性质可知ED⊥AB,∠DEA=∠BEA,然后可证明∠BED=∠ABC,最后根据锐角三角函数的定义求解即可.
【解答】解:由翻折的性质可知:ED⊥AB,∠DEA=∠BEA.
∵∠A+∠DEA=90°,∠CBA+∠A=90°,
∴∠DEA=∠CBA.
∴∠BED=∠CBA.
∴tan∠BED=tan∠CBA= =
= .
.
故答案为: .
.
【点评】本题主要考查的是翻折的性质、锐角三角函数的定义,证得∠BED=∠CBA是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
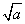 是同类二次根式的是……………( )
是同类二次根式的是……………( ) 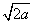 (B)
(B)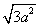 (C)
(C)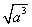 (D)
(D)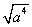
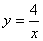 (
(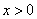 )的图象上,若阴影部分的面积为12 -
)的图象上,若阴影部分的面积为12 -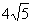 ,则点E的坐标是 .
,则点E的坐标是 . 
 ∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.
∥l2∥l3,AB=4,DF=8,BC=6,则DE=__________.
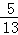 ,AB=13.
,AB=13.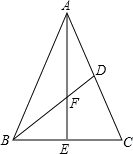
 ,其中a=3,b=﹣1.
,其中a=3,b=﹣1. 有意义的
有意义的 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.