题目内容
19. 已知△ABC的内接矩形EFGH的两个顶点E、F在BC边上,另外两个顶点H、G分别在AB、AC边上.
已知△ABC的内接矩形EFGH的两个顶点E、F在BC边上,另外两个顶点H、G分别在AB、AC边上.(1)设BC=12cm,高AD为h cm,GF=x cm,GH=y cm,求y关于x的函数关系式;
(2)在(1)的条件下,当高h=8cm时,要使矩形EFGH的GH边大于4cm,求GF的取值范围;
(3)在(1)、(2)的条件下,要使矩形EFGH的面积最大,则此矩形两边长分别是多少?
分析 (1)由四边形HEFG是矩形,得到HG∥BC,推出△AHG∽△ABC,得到比例式,代入数据即可得到结论;
(2)把h=8cm,GH>4,代入y=-$\frac{12x}{h}$+12;得到不等式-$\frac{12x}{8}+12>4$,解不等式即可得到结果;
(3)根据矩形的面积公式列方程,于是得到结论.
解答 解:(1)∵四边形HEFG是矩形,
∴HG∥EF,
∴HG∥BC,
∴△AHG∽△ABC,
∴$\frac{HG}{BC}$=$\frac{AD-GF}{AD}$,
即$\frac{y}{12}=\frac{h-x}{h}$,
∴y=-$\frac{12x}{h}$+12;
(2)∵h=8cm,GH>4,
∴-$\frac{12x}{8}+12>4$,
解得x<$\frac{16}{3}$,
∴GF的取值范围为:0<GF<$\frac{16}{3}$;
(3)∵S矩形EFGH=GH•GF=xy=(-$\frac{12x}{h}$+12)•x=-$\frac{3}{2}$x2+12x=-$\frac{3}{2}$(x-4)2+24,
∴要使矩形EFGH的面积最大,则此矩形两边长分别是4cm,6cm.
点评 本题考查的是相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
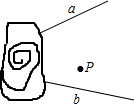 作图题:在图中a、b为已修好的两条铁路,铁路前方为未开辟的小山丘,现在要经过工厂P增筑一条铁路,且要求在开辟山丘后,新建的铁路能与a,b两铁路相交于一点,请你确定这条铁路的位置,画图说明.
作图题:在图中a、b为已修好的两条铁路,铁路前方为未开辟的小山丘,现在要经过工厂P增筑一条铁路,且要求在开辟山丘后,新建的铁路能与a,b两铁路相交于一点,请你确定这条铁路的位置,画图说明. 如图,AC=BG,AB,CG垂直平分线交于点F,求证:∠ABF=∠CGF.
如图,AC=BG,AB,CG垂直平分线交于点F,求证:∠ABF=∠CGF.