题目内容
4．设x1，x2是方程x2-2x-1=0的两个实数根，则$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值是（ ）| A． | -6 | B． | -5 | C． | -6或-5 | D． | 6或5 |
分析 先根据根与系数的关系得到x1+x2=2，x1x2=-1，然后利用整体代入的方法计算．
解答 解：根据题意得x1+x2=2，x1x2=-1，
所以$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{（{x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=-6．
故选A．
点评 本题考查了根与系数的关系，解题的关键是能够将代数式进行正确的变形，难度不大．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
14．估计$\sqrt{5}$+1的值在（ ）
| A． | 1和2之间 | B． | 2和3之间 | C． | 3和4之间 | D． | 4和5之间 |
15．
如图，从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A，B，C在圆周上，将剪下的扇形作为一个圆锥的侧面，则这个圆锥的底面圆的半径是（ ）
如图，从一块直径为4$\sqrt{2}$cm的圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A，B，C在圆周上，将剪下的扇形作为一个圆锥的侧面，则这个圆锥的底面圆的半径是（ ）| A． | 2$\sqrt{2}$cm | B． | $\sqrt{2}$cm | C． | 1 cm | D． | 2cm |
12．下列计算正确的是（ ）
| A． | a+a=a2 | B． | a•a2=a3 | C． | （-a3）2=a9 | D． | （3a）3=9a3 |
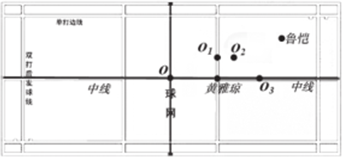2017 全英羽毛球公开赛混双决赛，中国组合鲁恺/黄雅琼，对阵马来西亚里约奥运亚军陈炳顺/吴柳萤，鲁恺/黄雅琼两名小将的完美配合结果获胜．如图是羽毛球场地示意图，x 轴平行场地的中线，y 轴平行场地的球网线，设定鲁恺的坐标是（3，1），黄雅琼的坐标是（0，-1），则坐标原点为（ ）
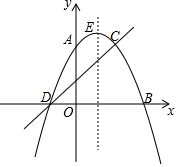如图，抛物线y=ax2+bx+c过A（0，4），B（4，0），C（2，4）三点，与x轴另一交点记作D，直线y=kx+n过C、D两点．
16．事件A：掷一次骰子，向上一面的点数是5；事件B：买一张彩票，有一注号码中奖了，则（ ）
| A． | 事件A和B都是随机事件 | |
| B． | 事件A是随机事件，事件B是不可能事件 | |
| C． | 事件A是必然事件，事件B是随机事件 | |
| D． | 事件A和事件B都是必然事件 |