题目内容
11. 计算:
计算:(1)如图所示,点B、C在线段AD上,点M是AB的中点,点N是CD的中点,若MN=11,BC=3,则AD的长为多少?
(2)已知一个角的补角比它的余角的3倍还多17°,求这个角的度数.
分析 (1)根据线段的和差,可得(MB+CN)的长,根据线段中点的性质,可得(AB+CD)的长,根据线段的和差,可得答案;
(2)设这个角为x,则补角为(180°-x),余角为(90°-x),再由补角比它的余角的3倍多17°,可得方程,解出即可.
解答 解:(1)由线段的和差,得
MB+CN=MN-BC=11-3=8,
由M是线段AB的中点,N是线段CD的中点,得
AB+CD=2MB+2CN=2(MB+CN)=16,
由线段的和差,得
AD=AB+BC+CD=16+3=19.
(2)设这个角为x,则补角为(180°-x),余角为(90°-x),
由题意得,180°-x=3(90°-x)+17°,
解得:x=53.5.
故这个角的度数是53.5°.
点评 本题考查了两点间的距离,利用了线段的和差,线段中点的性质.同时考查了余角和补角的知识,解答本题的关键是掌握互余的两角之和为90°,互补的两角之和为180°.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
20.下列计算正确的是( )
| A. | x2+x4=x6 | B. | x•x2=x3 | C. | x6÷x3=x2 | D. | (-x2y)2=x6y3 |
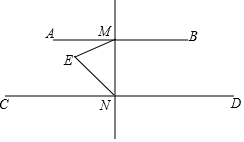 如图,AB∥CD,MN⊥AB于M.
如图,AB∥CD,MN⊥AB于M.