Question

8．某中学七（4）班一位学生针对七年级同学上学“出行方式”进行了一次调查．图（1）和图（2）是他根据采集的数据绘制的两幅不完整的统计图，请根据图中提供的信息解答以下问题：
（1）补全条形统计图，并计算出“骑车”部分所对应的圆心角的度数；
（2）如果全年级共800名同学，请估算全年级步行上学的学生人数；
（3）若由3名“乘车”的学生，1名“步行”的学生，2名“骑车”的学生组队参加一项活动，欲从中选出2人担任组长（不分正副），列出所有可能的情况，并求出2人都是“乘车”的学生的概率．

Answer 1

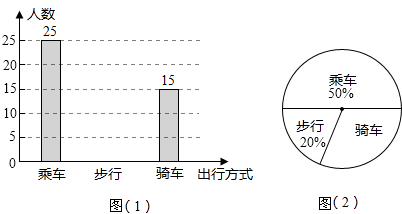
分析 （1）从两图中可以看出乘车的有25人，占了50%，所以共有学生50人；总人数减乘车的和骑车的就是步行的，根据数据画直方图就可；要求扇形的度数就要先求出骑车的占的百分比，然后再求度数；
（2）用这50人作为样本去估计该年级的步行人数．
（3）6人每2人担任班长，有15种情况，2人都是“喜欢乘车”的学生的情况有3种，然后根据概率公式即可求得．

解答 解：（1）25×2=50人；
50-25-15=10人；
如图所示条形图，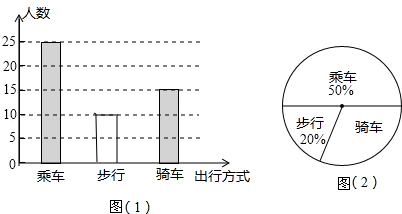

圆心角度数=$\frac{30}{100}$×360°=108°；
（2）估计该年级步行人数：800×20%=160（人）；
（3）设3名“乘车”的学生表示为A、B、C，1名“步行”的学生表示为D，2名“骑车”的学生表示为E，F，
则有：AB、AC、AD、AE、AF、BC、BD、BE、BF、CD、CE、CF、DE、DF、EF这15种等可能结果，
而2人都是“乘车”的结果有AB、AC、AD这3种，
故2人都是“乘车”的学生的概率P=$\frac{3}{15}=\frac{1}{5}$．

点评 本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．