题目内容
9．在平面直角坐标系xOy中，A点的坐标为（6，3），B点的坐标为（0，5），点M是x轴上的一个动点，则MA+MB的最小值是（ ）| A． | 8 | B． | 10 | C． | 12 | D． | 15 |
分析 先求出点A关于x轴对称的点A′的坐标，再用两点间的距离公式求出A′B的长即可．
解答 解：∵A点坐标为（6，3），
∴点A关于x轴对称的点A′（6，-3）．
∵B点坐标为（0，5），
∴A′B=$\sqrt{（6-0）^{2}+（-3-5）^{2}}$=10．
∴MA+MB的最小值为10．
故选：B．
点评 本题考查的是轴对称-最短路线问题，熟知两点之间，线段最短是解答此题的关键．
练习册系列答案
相关题目
如图，小亮在晚上由路灯A走向路灯B，当他走到点C时，发现身后他影子的顶部刚好接触到路灯A的底部，当他向前再步行12m到达点D时，发现身前他影子的顶部刚好接触到路灯B的底部．已知小亮的身高是1.5m，两个路灯的高度都是9m．当小亮走到路灯B时，他在路灯A下的影长是3.6m．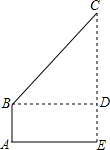
如图，小芳站在地面上A处放风筝，风筝飞到C处时的线长BC为23米，这时测得∠CBD=58°，牵引底端B与地面的距离BA为1.6米，求此时风筝离地面的高度CE．（结果精确到0.1米）（参考数据：sin58°=0.85，cos58°=0.53，tan58°=1.60）
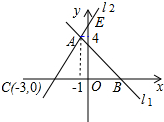如图，直线l1的解析式是y=-x+3，与直线l2交于点A，且两直线分别交x轴于点B，C，交y轴于点D，E．
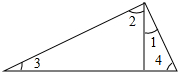如图，已知∠1+∠2=90°，∠2+∠3=90°