题目内容
如图，直线AB，CD相交于点O，OE分∠AOD成两个角，∠AOE：∠EOD=2：6，∠BOD-∠BOC=20°，求∠AOE的度数．考点：对顶角、邻补角
专题：
分析：根据邻补角，可得∠BOC，根据对顶角相等，可得∠AOD，再根据∠AOE：∠EOD，可得答案．
解答：解：由邻补角的定义，得∠BOC+∠BOD=180°①，∠BOD-∠BOC=20°②，
①-②得
2∠BOC=160°，解得∠BOC=80°，
由对顶角相等，得∠AOD=∠BOC=80°，
由∠AOE：∠EOD=2：6，得∠EOD=3∠AOE，
由角的和差，得∠AOE+∠EOD=∠AOD，即∠AOE+3∠AOE=80°，
解得∠AOE=20°．
①-②得
2∠BOC=160°，解得∠BOC=80°，
由对顶角相等，得∠AOD=∠BOC=80°，
由∠AOE：∠EOD=2：6，得∠EOD=3∠AOE，
由角的和差，得∠AOE+∠EOD=∠AOD，即∠AOE+3∠AOE=80°，
解得∠AOE=20°．
点评：本题考查了对顶角、邻补角，利用了邻补角的定义，对顶角的性质，角的和差．
练习册系列答案
相关题目
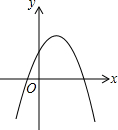二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①a＞0；②c＞0；③b2-4ac＞0，其中正确的是（ ）| A、②③ | B、①② | C、①②③ | D、①③ |
如图，矩形草坪长20米，宽10米，沿草坪三面有1米宽的小路，小路内外边缘所成的矩形相似吗？为什么？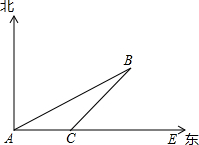
如图，一艘轮船由西向东航行，在A处测得小岛B在北偏东75°方向，又航行8海里后，在C处测得小岛B在北偏东60°方向，若小岛周围3.8海里范围内有暗礁，则该船一直向东航行有无触礁危险？