��Ŀ����
12�����Ķ�������$\frac{{\sqrt{3}}}{{\sqrt{3}-\sqrt{2}}}=\frac{{\sqrt{3}��\sqrt{3}+\sqrt{2}��}}{{��\sqrt{3}-\sqrt{2}����\sqrt{3}+\sqrt{2}��}}=\frac{{3+\sqrt{6}}}{{{{��\sqrt{3}��}^2}-{{��\sqrt{2}��}^2}}}=3+\sqrt{6}$����������������У�$\sqrt{3}$-$\sqrt{2}$��$\sqrt{3}$+$\sqrt{2}$��˻������ж��θ�ʽ�����ǿɽ�������ʽ�ӳ�Ϊ��Ϊ��������ʽ�������������Ҳ��Ϊ��ĸ��������
��1��$\sqrt{5}$+2����������ʽ��$\sqrt{5}$-2��
��2����$\frac{3}{{3+\sqrt{6}}}$���з�ĸ��������
���� ��1�����������ҳ�ԭʽ����������ʽ���ɣ�
��2����ԭʽ��ĸ���������ɵõ������
��� �⣺��1��$\sqrt{5}$+2����������ʽ��$\sqrt{5}$-2��
��2��ԭʽ=$\frac{3��3-\sqrt{6}��}{��3+\sqrt{6}����3-\sqrt{6}��}$=$\frac{9-3\sqrt{6}}{9-6}$=3-$\sqrt{6}$��
�ʴ�Ϊ����1��$\sqrt{5}$-2
���� ���⿼���˷�ĸ���������ҳ�ԭʽ����������ʽ�ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
7��ij������Ч���ܵƵ���������2010��Ϊ10��ֻ��Ԥ��2012�꽫�ﵽ14.4��ֻ����õ���2010�굽2012���Ч���ܵ�����������ƽ��������Ϊ��������
| A�� | 10% | B�� | 20% | C�� | 30% | D�� | 40% |
4����ͼ������ֽƬ��ͼ��1���е����ߵ�һ���۵���ͼ��2�����ۺ������һ�ߵ��γɵġ�1=65�㣬�ٰ�ͼ��2���е����߽��еڶ��۵��õ�ͼ��3�������2�Ķ���Ϊ��������
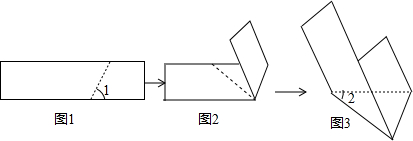

| A�� | 20�� | B�� | 25�� | C�� | 30�� | D�� | 35�� |
1������������ȷ���ǣ�������
| A�� | a2•a3=a6 | B�� | ��ab��3=ab3 | C�� | ��a2��3=a6 | D�� | a6��a2=a3 |
2�������ʽ$\frac{{x}^{2}-9}{3x+9}$��ֵΪ�㣬��x��ֵΪ��������
| A�� | 9 | B�� | 3 | C�� | -3 | D�� | ��3 |
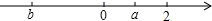 �����ᣬ����|a|-|b|+|a-2|��
�����ᣬ����|a|-|b|+|a-2|��