题目内容
1. 如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.
分析 (1)由BC=EF,∠B=∠DEF,∠ACB=∠F,即可根据ASA证明;
(2)欲证明四边形ACFD是平行四边形,只要证明AC=DF,AC∥DF即可;
解答 (1)证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=EC=CF,
∴BC=EF,
在△ABC和△DEF中
$\left\{\begin{array}{l}{∠B=∠DEF}\\{BC=EF}\\{∠ACB=∠F}\end{array}\right.$
∴△ABC≌△DEF(ASA).
(2)证明:∵△ABC≌△DEF
∴AC=DF,
∵∠ACB=∠F,
∴AC∥DF,
∴四边形ACFD是平行四边形.
点评 本题考查平行四边形的判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
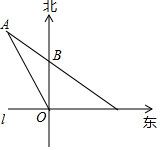 如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距60$\sqrt{3}$千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.
如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距60$\sqrt{3}$千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处. 如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数.
如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数. 已知,如图,点D是△ABC中AC边上的一点,点E是BC边延长线上一点,说明:∠ADB>∠CDE.
已知,如图,点D是△ABC中AC边上的一点,点E是BC边延长线上一点,说明:∠ADB>∠CDE.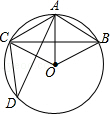 如图,在半径为6 cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BDC}$上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3$\sqrt{3}{cm}$;③∠AOB=60°;④四边形ABOC是菱形,其中正确结论的序号是①③④.
如图,在半径为6 cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BDC}$上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=3$\sqrt{3}{cm}$;③∠AOB=60°;④四边形ABOC是菱形,其中正确结论的序号是①③④.