题目内容
5.观察下列每对数在数轴上对应点间的距离:4与-2,3与5,-2与-6,-4与3.如:4与-2对应点间的距离是|4-(-2)|=6;3与5对应点间的距离是|3-5|=2.回答下列问题:
(1)若数轴上A、B两点分别表示有理数a、b,则A、B两点间的距离是多少?(用含a、b的式子表示)
答:|b-a|;
(2)若数轴上的点A表示的数为x,点B表示的数为-1,则A与B两点间的距离可以表示为|x+1|;
(3)结合数轴可得|x-2|+|x+3|的最小值为5;
(4)若关于x的方程|x-1|+|x+1|+|x-5|=a无解,则a的取值范围是a<6.
分析 (1)直接借助数轴可以得出;
(2)结合数轴,分三种情况进行讨论.当x<-1时,距离为-x-1,当-1<x<0时,距离为x+1,当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
(3)|x-2|即x与2的差的绝对值,它可以表示数轴上x与2之间的距离.|x+3|=|x-(-3)|即x与-3的差的绝对值,它也可以表示数轴上x与-3之间的距离. 借助数轴,我们可以得到正确答案;
(4)分情况讨论:①当x≥5时,②当1≤x<5时,③当-1≤x<1时,④当x<-1时,分别得出f(x)的取值范围,进而确定f(x)的取值范围,从而得出a的值.
解答 解:(1)由观察可知:A、B两点间的距离是|b-a|;
(2)结合数轴,我们发现应分以下三种情况进行讨论.
当x<-1时,距离为-x-1,
当-1<x<0时,距离为x+1,
当x>0,距离为x+1.综上,我们得到A与B两点间的距离可以表示为|x+1|;
(3)当x<-3时,|x-2|+|x+3|=2-x-(3+x)=-2x-1,此时最小值大于5;
当-3≤x≤2时,|x-2|+|x+3|=2-x+x+3=5;
当x>2时,|x-2|+|x+3|=x-2+x+3=2x+1,此时最小值大于5;
所以|x-2|+|x+3|的最小值为5,取得最小值时x的取值范围为-3≤x≤2;
(4)先求f(x)=|x-1|+|x+1|+|x-5|的值域:
当x≥5时,f(x)=x-1+x+1+x-5=3x-5≥10,
当1≤x<5时,f(x)=x-1+x+1+5-x=x+5,此时值域为[6,10),
当-1≤x<1时,f(x)=1-x+x+1+5-x=7-x,此时值域为(6,8],
当x<-1时,f(x)=1-x-x-1+5-x=5-3x>8,此时值域为(8,+∞),
所以f(x)的值域为:f(x)≥6.
即:|x-1|+|x+1|+|x-5|≥6,
因为|x-1|+|x+1|+|x-5|=a无解,
所以a<6.
故答案为:(1)|b-a|;(2)|x+1|;(3)5;(4)a<6.
点评 此题考查了数轴的有关知识,借助数轴可以使有关绝对值的问题转化为数轴上有关距离的问题,反之,有关数轴上的距离问题也可以转化为绝对值问题.这种相互转化在解决某些问题时可以带来方便.事实上,|A-B|表示的几何意义就是在数轴上表示数A与数B的点之间的距离.

| A. | 13.8111×104 | B. | 1.38111×106 | C. | 13.8111×105 | D. | 1.38111×105 |
| A. | 3 | B. | 7 | C. | -7 | D. | -3 |
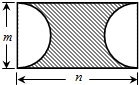 如图所示,阴影部分的面积为mn-$\frac{π{m}^{2}}{4}$(不化简也算对).
如图所示,阴影部分的面积为mn-$\frac{π{m}^{2}}{4}$(不化简也算对).