题目内容
8.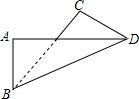 如图表示长方形纸片ABCD沿对角线BD折叠后的情况,图中有没有关于某条直线对称的图形?如有,请作出对称轴,有没有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角.
如图表示长方形纸片ABCD沿对角线BD折叠后的情况,图中有没有关于某条直线对称的图形?如有,请作出对称轴,有没有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角.
分析 如果一个图形沿着一条直线对折后,能够和另一个图形完全重合,这样的两个图形之间的关系叫轴对称,从而可得出所给图形中的轴对称图形及对称轴;再根据矩形的对边相等,及折叠前后三角形全等可得出图中的相等线段及相等角.
解答  解:关于某条直线对称的图形.
解:关于某条直线对称的图形.
过点E作EF⊥BD,则△ABD和△CDB关于EF对称,△ABE和△CDE关于EF对称.
相等的线段为:AB=CD,AE=CE,BE=ED,AD=BC.
相等的角为:∠ABD=∠CDB,∠CBD=∠ADB,∠ABE=∠CDE,∠AEB=∠CED.
点评 此题考查了翻折变换的性质及轴对称的性质,解答本题需要掌握轴对称的定义及翻折变换前后两图形全等,难度一般.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
16.下列计算正确的是( )
| A. | x6÷x2=x3 | B. | $3{m^{-2}}=\frac{1}{{3{m^2}}}$ | C. | (a3b)2=a6b2 | D. | (a2)4=a6 |
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )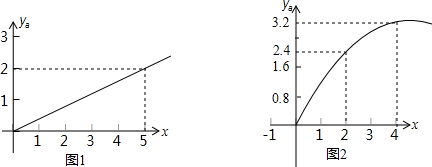
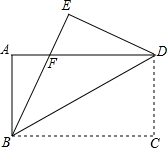 如图,沿矩形ABCD的对角线BD折叠,点C落在点E的位置,已知BC=8cm,AB=6cm,那么折叠后的重合部分的面积是多少?
如图,沿矩形ABCD的对角线BD折叠,点C落在点E的位置,已知BC=8cm,AB=6cm,那么折叠后的重合部分的面积是多少?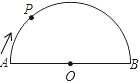 如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )
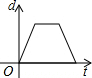
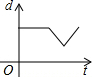
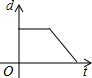
如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )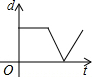
 如图,点A在反比例函数y=$\frac{4}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$(k<0)的图象上,且∠AOB=90°,tan∠OAB=$\frac{4}{3}$,则k的值是-$\frac{16}{9}$.
如图,点A在反比例函数y=$\frac{4}{x}$的图象上,点B在反比例函数y=$\frac{k}{x}$(k<0)的图象上,且∠AOB=90°,tan∠OAB=$\frac{4}{3}$,则k的值是-$\frac{16}{9}$.