题目内容
15.计算(1)($\sqrt{3}$-1)2-(2$\sqrt{3}$)2
(2)$\sqrt{32}$-5$\sqrt{\frac{1}{2}}$+6$\sqrt{\frac{1}{8}}$.
分析 (1)运用平方差公式分解,再去括号展开,最后合并同类二次根式即可;
(2)先化简各二次根式,再合并同类二次根式即可.
解答 解:(1)原式=($\sqrt{3}$-1+2$\sqrt{3}$)×($\sqrt{3}-1-2\sqrt{3}$)
=(3$\sqrt{3}$-1)×(-1-$\sqrt{3}$)
=-3$\sqrt{3}$-9+1+$\sqrt{3}$
=-2$\sqrt{3}$-8;
(2)原式=4$\sqrt{2}$-$\frac{5\sqrt{2}}{2}$+$\frac{3\sqrt{2}}{2}$
=4$\sqrt{2}$-$\sqrt{2}$
=3$\sqrt{2}$.
点评 本题主要考查二次根式的混合运算,熟练掌握二次根式混合运算的顺序和二次根式的相关性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.2015年10月17日是我国第二个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A、B两组捐款人数的比为1:5.
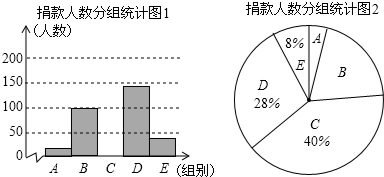
被调查的捐款人数分组统计表:
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?

被调查的捐款人数分组统计表:
| 组别 | 捐款额x/元 | 人数 |
| A | 1≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | 200 |
| D | 30≤x<40 | 140 |
| E | 40≤x | 40 |
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
5.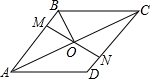 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |
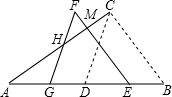 如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.
如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.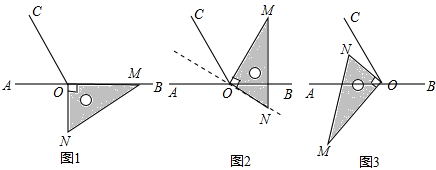
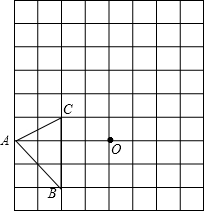 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算: