题目内容
3.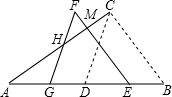 如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.
如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.(1)求证:AG=GH;
(2)求四边形GHME的面积.
分析 (1)根据平移的性质可得△BCD≌△EFG,FG∥CD,EF∥CB,DG=EB=1,再根据直角三角形的性质可得AD=CD=BD=$\frac{1}{2}$AB=$\frac{1}{2}×8$=4,然后再根据等边对等角,以及平行线的性质可得AG=GH;
(2)过C作CN⊥AB于N,证明△BCD为等边三角形,利用勾股定理计算出CN,根据直角三角形的性质计算出MF,HM,再表示出△FHM和△FGE的面积,求差即可.
解答 (1)证明:将△BCD沿BA方向平移得到△EFG,
∴△BCD≌△EFG,FG∥CD,EF∥CB,DG=EB=1,
∵∠ACB=90°,D是AB的中点,
∴AD=CD=BD=$\frac{1}{2}$AB=$\frac{1}{2}×8$=4,
∴∠DAC=∠ACD,
∵FG∥CD,
∴∠AFG=∠ACD,
∴∠AHG=∠DAC,
∴AG=GH;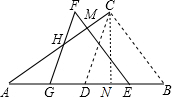
(2)解:如图:过C作CN⊥AB于N,
∵∠ABC=60°,∠ACB=90°,
∴∠A=30°,
∵BC=$\frac{1}{2}$AB=$\frac{1}{2}×8$=4,
∵∠ABC=60°,CD=BD,
∴△BCD为等边三角形,
∴NB=$\frac{1}{2}$BD=2,
∴CN=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵DG=1,AD=4,
∴GH=AG=3,
∴FH=1,
∵∠A=30°,
∴∠A=30°=∠AHG=∠FHM=30°,
∵FE∥CB,∠ACB=90°,
∴MF=$\frac{1}{2}$,
∴HM=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$.
∴S△EFG=S△BCD=$\frac{1}{2}×$4×2$\sqrt{3}$=4$\sqrt{3}$,
S△MFH=$\frac{1}{2}×\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$,
∴S四边形GHME=4$\sqrt{3}$-$\frac{\sqrt{3}}{8}$=$\frac{31\sqrt{3}}{8}$(cm2).
点评 此题主要考查了勾股定理的应用,以及直角三角形的面积,图形平移的性质,关键是掌握直角三角形的向关系性质.

| A. | p=-3,q=-10 | B. | p=-3,q=10 | C. | p=7,q=-10 | D. | p=7,q=10 |
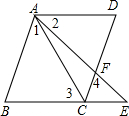 如图,已知AB∥CD,若∠1=∠2,∠3=∠4,则AD与BE平行吗?请说明理由.
如图,已知AB∥CD,若∠1=∠2,∠3=∠4,则AD与BE平行吗?请说明理由.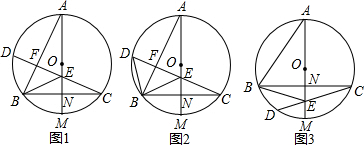
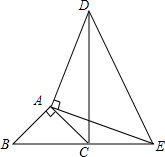 已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.
已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上. 下图是由7个相同的小正方体组成的几何体,则从上面看该几何体的平面图形是( )
下图是由7个相同的小正方体组成的几何体,则从上面看该几何体的平面图形是( )



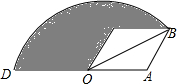 如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.
如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.