题目内容
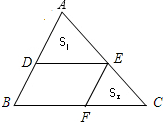如图，已知D、E、F分别在△ABC的三边上，DE∥BC，EF∥AB，记△ABC、△ADE、△EFC的面积分别为S，S1，S2．（1）求证：
| S1 |
| S2 |
| S |
（2）试用含S1，S2的代数式表示?DBFE的面积．
考点：相似三角形的判定与性质
专题：
分析：（1）证明△ADE∽△ABC，△CEF∽△ABC，得到S，S1，S2与线段AE、AC、CE之间的数量关系；列出比例式即可解决问题．
（2）将（1）中的结论两边平方，化简整理即可解决问题．
（2）将（1）中的结论两边平方，化简整理即可解决问题．
解答：解：（1）如图，∵DE∥BC，EF∥AB，
∴△ADE∽△ABC，△CEF∽△ABC，
∴
=(
)2，
=(
)2，
∴
+
=
+
=1，
∴
+
=
．
（2）∵
+
=
，
∴S1+S2+2
=S，
∴?DBFE的面积=S-S1-S2=2
．
解：（1）如图，∵DE∥BC，EF∥AB，∴△ADE∽△ABC，△CEF∽△ABC，
∴
| S1 |
| S |
| AE |
| AC |
| S2 |
| S |
| CE |
| AC |
∴
|
|
| AE |
| AC |
| CE |
| AC |
∴
| S1 |
| S2 |
| S |
（2）∵
| S1 |
| S2 |
| S |
∴S1+S2+2
| S1S2 |
∴?DBFE的面积=S-S1-S2=2
| S1S2 |
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是深入观察图形，正确找出命题图形中隐含的相似三角形，灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
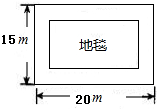一间会议室，它的地面是长方形的，长为20m，宽为15m，现在准备在会议室地面的中间铺一块地毯，要求四周未铺地毯的部分宽度相等，而且地毯的面积是会议室地面面积的一半，则地面上未铺地毯的部分宽度是多米？
如图，点C是线段AB上一点，且AC=2CB．D是AB的中点，E是CB的中点，DE=6，求：
如图所示，直线PD为△ABC一边BC的垂直平分线，点D为垂足，连接CP并延长CP交边AB于点F，射线BP交边AC于点E．