题目内容
 如图,点C是线段AB上一点,且AC=2CB.D是AB的中点,E是CB的中点,DE=6,求:
如图,点C是线段AB上一点,且AC=2CB.D是AB的中点,E是CB的中点,DE=6,求:(1)AB的长;
(2)AD:CB的值.
考点:两点间的距离
专题:计算题
分析:(1)设BC=x,由AC=2CB得到AC=2x,则AB=AC+BC=3x,再由D是AB的中点得到AD=BD=
x,则可计算出DC=BD-BC=
x,然后利用E是CB的中点得到CE=
BC=
x,于是可利用DC+CE=DE得到
x+
x=6,解方程求出x,再计算3x即可得到AB的长;
(2)利用AD=
x,BC=x可计算AD:BC的比值.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用AD=
| 3 |
| 2 |
解答:解:(1)设BC=x,
∵AC=2CB,
∴AC=2x,
∴AB=AC+BC=3x,
∵D是AB的中点,
∴AD=BD=
AB=
x,
∴DC=BD-BC=
x-x=
x,
∵E是CB的中点,
∴CE=
BC=
x,
而DC+CE=DE,
∴
x+
x=6,解得x=6,
∴AB=3x=18;
(2)∵AD=
x,BC=x,
∴AD:BC=
x:x=3:2.
∵AC=2CB,
∴AC=2x,
∴AB=AC+BC=3x,
∵D是AB的中点,
∴AD=BD=
| 1 |
| 2 |
| 3 |
| 2 |
∴DC=BD-BC=
| 3 |
| 2 |
| 1 |
| 2 |
∵E是CB的中点,
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
而DC+CE=DE,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=3x=18;
(2)∵AD=
| 3 |
| 2 |
∴AD:BC=
| 3 |
| 2 |
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.可以说画线段,但不能说画距离.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
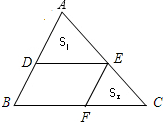 如图,已知D、E、F分别在△ABC的三边上,DE∥BC,EF∥AB,记△ABC、△ADE、△EFC的面积分别为S,S1,S2.
如图,已知D、E、F分别在△ABC的三边上,DE∥BC,EF∥AB,记△ABC、△ADE、△EFC的面积分别为S,S1,S2.