题目内容
8. 如图,△ABC是等边三角形,点D为AC边上一点,以BD为边作等边△BDE,连接CE,若CD=1,CE=4,则BC=5.
如图,△ABC是等边三角形,点D为AC边上一点,以BD为边作等边△BDE,连接CE,若CD=1,CE=4,则BC=5.
分析 根据等边三角形的性质可得AB=BC,BD=BE,∠ABC=∠DBE=60°,再求出∠ABD=∠CBE,然后利用“边角边”证明△ABD和△CBE全等,根据全等三角形对应边相等可得AD=CE,然后求出AC,再根据等边三角形的性质可得BC=AC.
解答 解:∵△ABC,△BDE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABC-∠CBD=∠DBE-∠CBD,
即∠ABD=∠CBE,
在△ABD和△CBE中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBE}\\{BD=BE}\end{array}\right.$,
∴△ABD≌△CBE(SAS),
∴AD=CE,
∵CD=1,CE=4,
∴AC=AD+CD=CE+CD=4+1=5,
∵△ABC是等边三角形,
∴BC=AC=5.
故答案为:5.
点评 本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握三角形全等的判定以及等边三角形的性质是解题的关键.

练习册系列答案
相关题目
19. 如果点A、B、C、D所对应的数为a、b、c、d,则a、b、c、d的大小关系是( )
如果点A、B、C、D所对应的数为a、b、c、d,则a、b、c、d的大小关系是( )
 如果点A、B、C、D所对应的数为a、b、c、d,则a、b、c、d的大小关系是( )
如果点A、B、C、D所对应的数为a、b、c、d,则a、b、c、d的大小关系是( )| A. | a<c<d<b | B. | b<d<a<c | C. | b<d<c<a | D. | d<b<c<a |
16.下列各组数中,互为倒数的是( )
| A. | -0.15和$\frac{20}{3}$ | B. | -3和$\frac{1}{3}$ | C. | 0.01和100 | D. | 1和-1 |
13. 如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )
如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )
 如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )
如图,正方形ABCD的边长为2,O是边AB上一动点,以O为圆心,2为半径作圆,分别与AD、BC相交于M、N,则扇形OMN的面积S的范围是( )| A. | $\frac{2}{3}$π≤s≤π | B. | $\frac{1}{2}$π≤s≤π | C. | $\frac{\sqrt{3}}{3}$π≤s≤π | D. | 0≤s≤π |
 已知直线l的表达式为y=-x+8,与x轴交于点B,点P(x,y)在直线l上,且x>0,y>0,点A的坐标为(6,0).
已知直线l的表达式为y=-x+8,与x轴交于点B,点P(x,y)在直线l上,且x>0,y>0,点A的坐标为(6,0).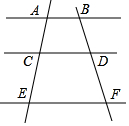 如图,AB∥CD∥EF,如果AC=2,AE=5.5,DF=3,那么BD=$\frac{12}{7}$.
如图,AB∥CD∥EF,如果AC=2,AE=5.5,DF=3,那么BD=$\frac{12}{7}$.