题目内容
19.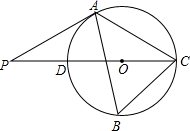 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求∠P的度数;
(2)求证:PA是⊙O的切线;
(3)若PD=$\sqrt{3}$,求⊙O的直径.
分析 (1)连结AD,如图,根据圆周角定理得∠DAC=90°,∠ADC=∠B=60°,则利用三角形内角和定理得∠ACD=30°,由于AP=AC,于是利用等腰三角形的性质易得∠P=30°;
(2)连结OA,如图,先判断△OAD为等边三角形,则∠DOA=60°,而∠P=30°,则可计算出∠OAP=90°,然后根据切线的判定定理得到PA是⊙O的切线;
(3)在Rt△APO中,根据含30度的直角三角形三边的关系得到OA=$\frac{1}{2}$OP,即OD+PD=2OA,而OD=OA,于是有OA=PD=$\sqrt{3}$,从而得到圆的直径.
解答  (1)解:连结AD,如图,
(1)解:连结AD,如图,
∵CD是⊙O的直径,
∴∠DAC=90°,
∵∠ADC=∠B=60°,
∴∠ACD=30°,
∵AP=AC,
∴∠P=∠ACP=30°;
(2)证明:连结OA,如图,
∵OD=OA,∠ADO=60°,
∴△OAD为等边三角形,
∴∠DOA=60°,
而∠P=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴PA是⊙O的切线;
(3)解:在Rt△APO中,∵∠P=30°,
∴OA=$\frac{1}{2}$OP,即OD+PD=2OA,
而OD=OA,
∴OA=PD=$\sqrt{3}$,
∴⊙O的直径为2$\sqrt{3}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的性质和圆周角定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知二次函数y=x2+2x-k,小聪利用计算器列出了下表:
那么方程x2+2x-k=0的一个近似根是( )
| x | -4.1 | -4.2 | -4.3 | -4.4 |
| x2+2x-k | -1.39 | -0.76 | -0.11 | 0.56 |
| A. | -4.1 | B. | -4.2 | C. | -4.3 | D. | -4.4 |
4.⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.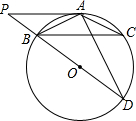 如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.
如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD. 综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为17米.
综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为17米.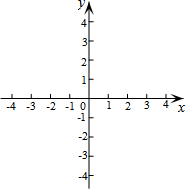 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-1,3),B(-3,2),C(0,1).画出△ABC,并画出关于原点O对称的△A1B1C1.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-1,3),B(-3,2),C(0,1).画出△ABC,并画出关于原点O对称的△A1B1C1.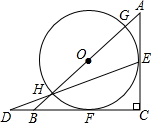 如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.
如图,在等腰直角三角形△ABC中,∠ACB=90°,以斜边AB上的点O为圆心的圆分别与AC、BC相切于E、F,与AB分别交于点G、H,且EH的延长线和CB的延长线交于点D.