题目内容
12. 某校6名学生的体育成绩统计如图,这6名学生的体育成绩的方差是( )
某校6名学生的体育成绩统计如图,这6名学生的体育成绩的方差是( )| A. | 5 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{14}{9}$ |
分析 先利用折线统计图得到6个数据,再计算数据的平均数,然后根据方差公式求解.
解答 解:由折线统计图得6名学生的体育成绩为:17,17,18,18,18,20,
平均数=$\frac{17×2+18×3+20}{6}$=18,
所以这6名学生的体育成绩的方差S2=$\frac{1}{6}$[(17-18)2+(17-18)2+[(18-18)2+(18-18)2+(18-18)2+(20-18)2]=1.
故选B.
点评 本题考查了方差:一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差,计算公式是:s2=$\frac{1}{n}$[(x1-x?)2+(x2-x?)2+…+(xn-x?)2].也考查了折线统计图.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图,EB=EC,AB=AC,则此图中全等三角形有( )
如图,EB=EC,AB=AC,则此图中全等三角形有( )
 如图,EB=EC,AB=AC,则此图中全等三角形有( )
如图,EB=EC,AB=AC,则此图中全等三角形有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
20.$\frac{{\sqrt{x+1}}}{{\sqrt{x}}}$有意义的条件是( )
| A. | x≥-1 | B. | x>0 | C. | x>-1 | D. | x≥0 |
4.如果不等式组$\left\{\begin{array}{l}{-4x+1<-8-x}\\{x>m}\end{array}\right.$的解集是x>m,那么m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m=3 | D. | m<3 |
2.下列方程中,是关于x的一元二次方程为( )
| A. | 3x+1=5x+7 | B. | $\frac{1}{{x}^{2}}$+x-1=0 | ||
| C. | x2-5=0 | D. | ax2-bx=5(a和b为常数) |
 如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是4$\sqrt{5}$cm.
如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是4$\sqrt{5}$cm. 如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:△AFD≌△CEB.
如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.求证:△AFD≌△CEB.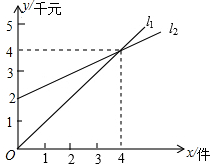 如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.
如图,l1、l2分别表示某种产品的销售收入与销售件数的函数关系图象和销售成本与件数的函数关系图象.