题目内容
6.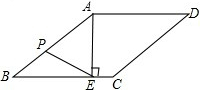 如图,在菱形ABCD中,AE⊥BC,点E为垂足.若cosB=$\frac{12}{13}$,EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是$\frac{120}{13}$.
如图,在菱形ABCD中,AE⊥BC,点E为垂足.若cosB=$\frac{12}{13}$,EC=2,P是AB边上的一个动点,则线段PE的长度的最小值是$\frac{120}{13}$.
分析 根据垂线段最短可知当EP⊥AB时,线段EP最短.根据$\frac{1}{2}$•AB•PE=$\frac{1}{2}$×BE×AE,只要求出AB、AE、BE即可解决问题.
解答 解:根据垂线段最短可知当EP⊥AB时,线段EP最短.
∵AE⊥BC于E,cosB=$\frac{BE}{AB}$=$\frac{12}{13}$,
设BE=12k,AB=BC=13k,则EC=k,
∵EC=2,
∴k=2,
∴BE=24,AB=26,AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=10,
当EP⊥AB时,$\frac{1}{2}$•AB•PE=$\frac{1}{2}$×BE×AE,
∴PE=$\frac{120}{13}$.
∴线段PE的最小值为$\frac{120}{13}$.
故答案为$\frac{120}{13}$.
点评 本题考查菱形的性质、解直角三角形、垂线段最短、锐角三角函数等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.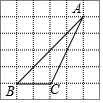 在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
 在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
在正方形网格中,△ABC的位置如图所示,则tanB的值为( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
18.2016年上半年,天津市生产总值8500.91亿元,按可比价格计算,同步增长9.2%,将“8500.91”用科学记数法可表示为( )
| A. | 8.50091×103 | B. | 8.50091×1011 | C. | 8.50091×105 | D. | 8.50091×1013 |
14.如图,正确表示数轴的是( )
| A. |  | B. |  | C. |  | D. |  |


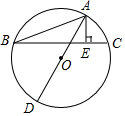 如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长.
如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长. 如图,将?ABCD的对角线BD向两个方向延长,分别至点E和点F,BE=DF.求证:四边形AECF是平行四边形.
如图,将?ABCD的对角线BD向两个方向延长,分别至点E和点F,BE=DF.求证:四边形AECF是平行四边形.