题目内容
5. 如图,在△ABC中,∠A=90°,E为BC上一点,A和E关于BD对称,B点和C点关于DE对称,则∠C的度数为30°.
如图,在△ABC中,∠A=90°,E为BC上一点,A和E关于BD对称,B点和C点关于DE对称,则∠C的度数为30°.
分析 借助轴对称的性质,A点和E点关于BD对称,有∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD,B点、C点关于DE对称,可得∠DBE=∠BCD,结合上式可得:∠ABC=2∠BCD,且∠ABC+∠BCD=90°,进而求得∠C的值.
解答 解:∵A点和E点关于BD对称,
∴∠ABD=∠EBD,即∠ABC=2∠ABD=2∠EBD.
又B点、C点关于DE对称,
∴∠DBE=∠C,∠ABC=2∠C.
∵∠A=90°,
∴∠ABC+∠C=2∠C+∠C=3∠C=90°.
∴∠C=30°,
故答案为:30°.
点评 本题考查轴对称的性质与运用.对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列各式没有意义的是( )
| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{-5}$ | D. | $\sqrt{(-5)^{2}}$ |
17.已知x+$\frac{1}{x}$=5,则${x^2}+\frac{1}{x^2}$的值为( )
| A. | 9 | B. | 5 | C. | 23 | D. | 25 |
 如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
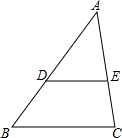 如图,若DE∥BC,CE=$\frac{2}{3}$AE,AB=20,则AD=12.
如图,若DE∥BC,CE=$\frac{2}{3}$AE,AB=20,则AD=12.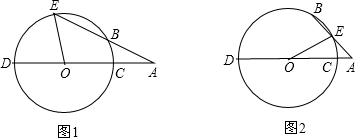
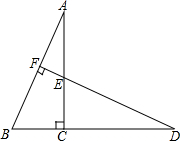 如图,△ABC中,∠ACB=90°,D是BC延长线上一点,DF⊥AB于F,DF交AC于E,找一找,图中有多少个直角三角形?与∠A相等的角有哪些?与∠A互余的角有哪些?请分别写出来.
如图,△ABC中,∠ACB=90°,D是BC延长线上一点,DF⊥AB于F,DF交AC于E,找一找,图中有多少个直角三角形?与∠A相等的角有哪些?与∠A互余的角有哪些?请分别写出来.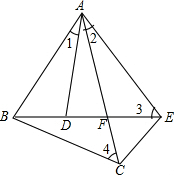 如图,已知∠1=∠2,∠3=∠4,求证:△ABD∽△ACE.
如图,已知∠1=∠2,∠3=∠4,求证:△ABD∽△ACE.