题目内容
8.2016年中秋节期间,某商城隆重开业,某商家有计划选购甲、乙两种礼盒作为开业期间给予买家的礼品,已知甲礼盒的单价是乙礼盒单价的1.5倍;用600元单独购买甲种礼盒比单独购买乙种礼盒要少10个.(1)求甲、乙两种礼盒的单价分别为多少元?
(2)若商家计划购买这两种礼盒共40个,且投入的经费不超过1050元,则购买的甲种礼盒最多买多少个?
分析 (1)根据题意可以得到相应的分式方程,从而可以解答本题;
(2)根据题意可以得到相应的不等式,从而可以解答本题.
解答 解:(1)设乙种礼盒购买了x个
$\frac{600}{1.5x}+10=\frac{600}{x}$,
解得,x=20,
经检验x=20是原分式方程的解,
则1.5x=30,
即甲、乙两种礼盒的单价分别为30元、20元;
(2)设购买甲种礼盒x个,
30x+20(40-x)≤1050,
解得,x≤25
即购买的甲种礼盒最多买25个.
点评 本题考查分式方程的应用、一元一次不等式的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16.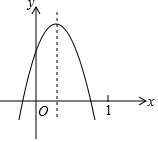 已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:
已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:
①abc<0;?②b2-4ac<0;?③2a+b>0;④a-b+c<0,其中正确的个数( )
 已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:
已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:①abc<0;?②b2-4ac<0;?③2a+b>0;④a-b+c<0,其中正确的个数( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.如果A(2,y1),B(3,y2)两点都在反比例函数y=$\frac{1}{x}$的图象上,那么y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | y1≥y2 |
20.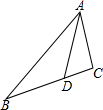 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
7.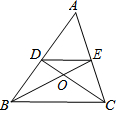 如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )
如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )
 如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )
如图,△ABC的两条中线BE、CD交于O,则S△EDO:S△ADE=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:6 |