题目内容
16.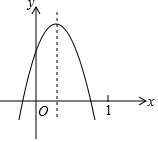 已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:
已知二次函数 y=ax2+bx+c (a≠0)的图象如图所示,则下列结论:①abc<0;?②b2-4ac<0;?③2a+b>0;④a-b+c<0,其中正确的个数( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①观察二次函数图象即可得出a<0、b>0、c>0,由此可得出abc<0,即①正确;②由抛物线与x轴有两个交点,由此可得出△=b2-4ac>0,即②错误;③由①可知0<b<-2a,由此可得出2a+b<0,即③错误;④观察函数图象可知当x=-1时,y=a-b+c<0,即④正确.综上即可得出结论.
解答 解:①观察二次函数图象可得出:a<0,0<-$\frac{b}{2a}$<1,c>0,
∴0<b<-2a,
∴abc<0,①正确;
②∵二次函数图象与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2-4ac>0,②错误;
③∵0<b<-2a,
∴b-(-2a)=2a+b<0,③错误;
④当x=-1时,y=a-b+c<0,④正确.
综上所述:正确的结论为①④.
故选C.
点评 本题考查了二次函数图象与系数的关系,观察二次函数图象找出a<0、0<b<-2a、c>0是解题的关键.

练习册系列答案
相关题目
7.下列各组式子中,为同类项的是( )
| A. | 5x2y 与-2xy2 | B. | 4x与4x2 | C. | -3xy与$\frac{3}{2}$yx | D. | 6x3y4与-6x3z4 |
5.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a3•a2=a6 | C. | (a2)3=a6 | D. | (a+b)2=a2+b2 |
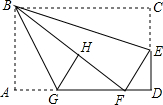 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: 按照下列要求完成作图及问题解答.
按照下列要求完成作图及问题解答.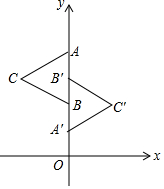 如图,正三角形ABC与正三角形A′B′C′关于某点成中心对称,已知A、B′、B三点的坐标分别是(0,4)、(0,3)、(0,2).
如图,正三角形ABC与正三角形A′B′C′关于某点成中心对称,已知A、B′、B三点的坐标分别是(0,4)、(0,3)、(0,2).