题目内容
一个正方体的对角线垂直于投影面,正方体的正投影是一个面积为25
的矩形,则该正方体的体积是 ,表面积是 .
| 2 |
考点:平行投影
专题:
分析:首先根据正方体的对角线垂直于投影面确定该正方体是如何放置的,然后根据其正投影的面积确定其棱长,从而确定其体积与表面积.
解答:解:对角面垂直于投影面,说明正方是以某一条棱贴地,然后侧面也地面成45°角放置的.
∵正投影是一个面积为25
的矩形,
∴矩形的宽就是棱长,长是棱长的
倍.
设棱长为a,则
a×
a=25
,
∴a=5,
∴体积是125,表面积是150.
故答案为:125,150.
∵正投影是一个面积为25
| 2 |
∴矩形的宽就是棱长,长是棱长的
| 2 |
设棱长为a,则
a×
| 2 |
| 2 |
∴a=5,
∴体积是125,表面积是150.
故答案为:125,150.
点评:本题考查了平行投影的知识,解题的关键是确定正方体是如何放置的,难度不大.

练习册系列答案
相关题目
下面的图形中是正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
下列式子是分式的是( )
A、2x2+
| ||
B、
| ||
C、
| ||
D、
|
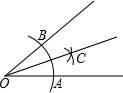 如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )
如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
a、b为任何非零有理数,则
+
+
的可能取值是( )
| a |
| |a| |
| b |
| |b| |
| ab |
| |ab| |
| A、-3或1 | B、3或1或-1 |
| C、1或3 | D、-1或3 |