题目内容
9.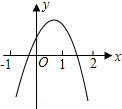 抛物线y=ax2+bx+c图象如图所示,则一次函数y=-bx-4ac+b2与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系内的图象大致为( )
抛物线y=ax2+bx+c图象如图所示,则一次函数y=-bx-4ac+b2与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系内的图象大致为( )| A. | 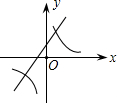 | B. | 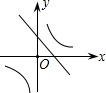 | C. | 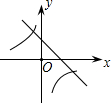 | D. | 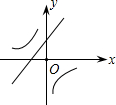 |
分析 先根据二次函数y=ax2+bx+c的图象判断出a、b、c、b2-4ac,a-b+c的符号,再用排除法对四个答案进行逐一检验.
解答  解:如图所示,抛物线y=ax2+bx+c的开口方向向下,则a<0.
解:如图所示,抛物线y=ax2+bx+c的开口方向向下,则a<0.
对此轴在y轴的右侧,则a、b异号,即b>0,所以-b<0.
抛物线与x轴有2个不同的交点,则b2-4ac>0,
所以一次函数y=-bx-4ac+b2经过第一、二、四象限.
又当x=-1时,y<0,即a-b+c<0,
所以反比例函数y=$\frac{a-b+c}{x}$经过第二、四象限.
综上所述,一次函数y=-bx-4ac+b2经过第一、二、四象限.反比例函数y=$\frac{a-b+c}{x}$经过第二、四象限.
故选:C.
点评 此题比较复杂,综合考查了二次函数、一次函数及反比例函数图象的特点,锻炼了学生数形结合解题的思想方法.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
17.下列运算正确的是( )
| A. | a3•a3=2a3 | B. | a4-a2=a2 | C. | (-x)5÷(-x)3=-x2 | D. | (a-b)2(b-a)3=(b-a)5 |
4.方程x2-7x+12=0的解为( )
| A. | 3或4 | B. | -3或-4 | C. | -3或4 | D. | 3或-4 |
18.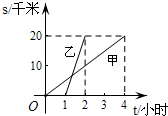 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )| A. | 甲的速度是4千米/小时 | B. | 乙的速度是10千米/小时 | ||
| C. | 乙比甲晚出发1小时 | D. | 甲比乙晚到B地3小时 |
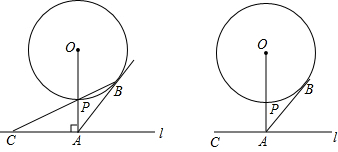
 如图,在矩形ABCD中,已知AB=6cm,BC=8cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为$\frac{10}{3}$πcm.(结果保留π)
如图,在矩形ABCD中,已知AB=6cm,BC=8cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为$\frac{10}{3}$πcm.(结果保留π) 如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.则这组数据的中位数是30.
如图是2012年伦敦奥运会吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.则这组数据的中位数是30.