题目内容
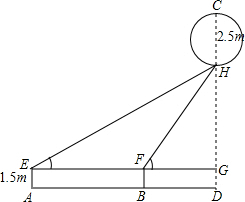 在一次数学试验活动中,为了测量空中一个静止的广告气球的高度,从地面点A用测角器测得H的仰角为30°,再沿直线AD前进20米到达点B,在地面B又用测角器测得点H的仰角为60°,已知气球自身的高CH为2.5米,测角器的高为1.5米,球气球顶部离地面的高度CD(结果保留根号).
在一次数学试验活动中,为了测量空中一个静止的广告气球的高度,从地面点A用测角器测得H的仰角为30°,再沿直线AD前进20米到达点B,在地面B又用测角器测得点H的仰角为60°,已知气球自身的高CH为2.5米,测角器的高为1.5米,球气球顶部离地面的高度CD(结果保留根号).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:先求出∠EHF的度数,再由等腰三角形的性质得出EF=HF,根据锐角三角函数的定义可得出GH的长,根据CD=DG+GH+HC即可得出结论.
解答:解:∵∠HEF=3O°,∠HFG=60°,
∴∠EHF=30°,
∴FH=EF=20米,
在Rt△HFG中,GH=HF•sin60°=20×
=10
米,
∴CD=DG+GH+HC=1.5+10
+2.5(=5+10
)米.
∴∠EHF=30°,
∴FH=EF=20米,
在Rt△HFG中,GH=HF•sin60°=20×
| ||
| 2 |
| 3 |
∴CD=DG+GH+HC=1.5+10
| 3 |
| 3 |
点评:本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x2+2x-1与x+m的乘积中不含x的一次项,则m的值为( )
| A、2 | ||
| B、-2 | ||
C、-
| ||
D、
|
 如图,EF∥MN,直线l分别与直线EF,MN相交,点A在直线EF上,点B在直线M上,且A,B都在l的左侧;点C在l上,但不在直线EF,MN上.设直线AC与EF所夹的锐角为∠FAC,直线BC与MN所夹的锐角为∠NBC.
如图,EF∥MN,直线l分别与直线EF,MN相交,点A在直线EF上,点B在直线M上,且A,B都在l的左侧;点C在l上,但不在直线EF,MN上.设直线AC与EF所夹的锐角为∠FAC,直线BC与MN所夹的锐角为∠NBC.