Question

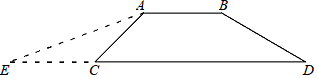
5．如图，AB⊥BC，CD⊥BC，垂足分别为B、C，AB=BC，E为BC的中点，且AE⊥BD于F，若AB=18cm，求CD的长度．

Answer 1

分析 如图，证明△ABE≌△BCD，得到BE=CD；结合AB=BC=2BE，即可解决问题．

解答 解：如图，∵AB⊥BC，AE⊥BD，
∴∠A+∠FEB=∠FBE+∠FEB，
∴∠A=∠FEB；
∵AB⊥BC，CD⊥BC，
∴∠ABE=∠BCD；
在△ABE与△BCD中，
$\left\{\begin{array}{l}{∠A=∠DBC}\\{AB=BC}\\{∠ABE=∠BCD}\end{array}\right.$，
∴△ABE≌△BCD（ASA），
∴BE=CD；AB=BC=18cm；
而点E为BC的中点，
∴BE=EC=CD=9（cm）．

点评 该题主要考查了全等三角形的判定及其性质的应用问题；解题的关键是深入观察图形，找出图形中隐含的等量关系或全等关系．