题目内容
6.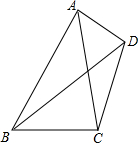 如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AC=6,BD=8,AC与BD所夹锐角为60°,则四边形ABCD的面积为( )| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24 | D. | 24$\sqrt{3}$ |
分析 作AE⊥BD于E,CF⊥BD于F,由于AC、BD夹角为θ,所以AE=OA•sinθ,CF=OC•sinθ,根据S四边形ABCD=S△ABD+S△BDC=$\frac{1}{2}$BD•AE+$\frac{1}{2}$BD•CF=$\frac{1}{2}$BD•(AE+CF )可以求出面积.
解答 作AE⊥BD于E,CF⊥BD于F,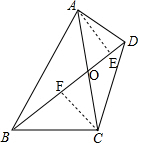
由于AC、BD夹角为θ,
所以AE=OA•sin60°,CF=OC•sin60°,
∴S四边形ABCD=S△ABD+S△BDC
=$\frac{1}{2}$BD•AE+$\frac{1}{2}$BD•CF
=$\frac{1}{2}$BD•(AE+CF)=$\frac{1}{2}$×8×6×sin60°=12$\sqrt{3}$.
故选:B.
点评 本题考查了三角形的面积,解直角三角形,通过解直角三角函数求得三角形的高是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.已知二次函数y=x2-x+a的图象与x轴的两个不同交点到原点的距离之和不超过5,则实数a的取值范围是( )
| A. | 0≤a<$\frac{1}{4}$ | B. | -6≤a<0 | C. | -5<a≤$\frac{1}{4}$ | D. | -6≤a<$\frac{1}{4}$ |
2.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.在方程x-$\frac{1}{5}$y=$\frac{3}{5}$中,用含x的代数式表示y,则( )
| A. | y=5x-3 | B. | y=-x-3 | C. | y=5x+3 | D. | y=-5x-3 |
16.在下列黑体大写英文字母中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
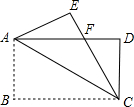 如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,连结ED,若AB=$\sqrt{3}$,BC=3.
如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,连结ED,若AB=$\sqrt{3}$,BC=3. 如图,该图的周长是28cm.
如图,该图的周长是28cm.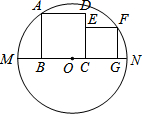 如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.
如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.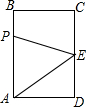 如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.