题目内容
4. 如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
分析 过点A作AE⊥CD于点E,根据正切的定义分别求出DE、CE,结合图形计算即可.
解答 解:过点A作AE⊥CD于点E,则四边形AEDB是矩形,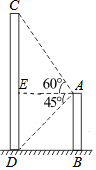
∴AB=DE,AE=DB=20米,
在Rt△ADE中,tan45°=$\frac{DE}{AE}$,
∴DE=AE=20,
在Rt△ACE中,tan60°=$\frac{CE}{AE}$,
∴CE=20$\sqrt{3}$,
∴CD=DE+CE=20+20$\sqrt{3}$≈55米,
答:大楼AB的高度是20米,大楼CD的高度约为55米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
19.在方程x-$\frac{1}{5}$y=$\frac{3}{5}$中,用含x的代数式表示y,则( )
| A. | y=5x-3 | B. | y=-x-3 | C. | y=5x+3 | D. | y=-5x-3 |
9.如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1)剩余部分虚线又剪拼成一个矩形(不重叠无缝隙),则该矩形的面积是( )cm2
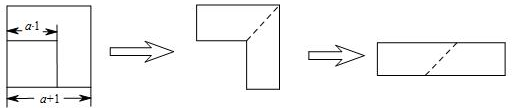

| A. | 2 | B. | 2a | C. | 4a | D. | (a2-1) |
16.在下列黑体大写英文字母中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
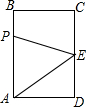 如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
如图,长方形ABCD中,AB=4cm,BC=3cm,E为CD的中点.动点P从A点出发,以每秒1cm的速度沿A-B-C-E运动,最终到达点E.若点P运动的时间为x秒,则当x=$\frac{10}{3}$或5时,△APE的面积等于5.
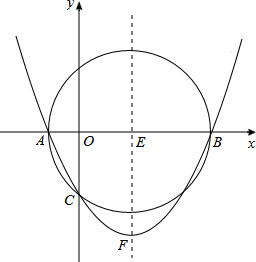 如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.
如图,以E(3,0)为圆心,5为半径的⊙E与x轴交于A、B两点,与y轴交于C点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,顶点为F.