题目内容
14. 如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.
如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.
分析 首先设AB为3xcm,BC为4xcm,AC为5xcm,利用方程求出三角形的三边,由勾股定理的逆定理得出三角形为直角三角形.再求出3秒后的,BP,BQ的长,利用三角形的面积公式计算求解.
解答 解:设AB为3xcm,BC为4xcm,AC为5xcm,
∵周长为36cm,
AB+BC+AC=36cm,
∴3x+4x+5x=36,
解得x=3,
∴AB=9cm,BC=12cm,AC=15cm,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,BP=9-3×1=6(cm),BQ=2×3=6(cm),
∴S△PBQ=$\frac{1}{2}$BP•BQ=$\frac{1}{2}$×(9-3)×6=18(cm2).
故答案为:18.
点评 此题主要考查了勾股定理逆定理、三角形的面积.由勾股定理的逆定理得出三角形为直角三角形,是解题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
19.已知一个二元一次方程组的解是$\left\{\begin{array}{l}x=-1\\ y=-2\end{array}\right.$,则这个方程组是( )
| A. | $\left\{\begin{array}{l}2x=y\\ x+y=-3\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=-3\\ x-2y=1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x+y=-3\\ x-y=-2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=0\\ 3x-y=5\end{array}\right.$ |
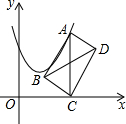 已知抛物线的顶点(1,1)抛物线与y轴交于点(0,2),点A为抛物线上一动点.
已知抛物线的顶点(1,1)抛物线与y轴交于点(0,2),点A为抛物线上一动点.
 由若干个大小相同的小正方体搭成的几何体,从正面和从上面看到的形状图如图所示,则组成这个几何体的小正方体的个数最多是11.
由若干个大小相同的小正方体搭成的几何体,从正面和从上面看到的形状图如图所示,则组成这个几何体的小正方体的个数最多是11.