题目内容
3.已知函数y=(m+2)${x}^{{m}^{2}+m-4}$+1是关于x的二次函数.(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
分析 (1)利用二次函数的定义得出关于m的等式进而得出答案;
(2)利用二次函数的性质得出m的值;
(3)利用二次函数的性质得出m的值.
解答 解:(1)∵函数y=(m+2)${x}^{{m}^{2}+m-4}$+1是关于x的二次函数,
∴m2+m-4=2,
解得:m1=2,m2=-3;
(2)当m=2时,抛物线有最低点,
此时y=4x2+1,
则最低点为:(0,1),
当x>0时,y随x的增大而增大;
(3)当m=-3时,函数有最大值,
此时y=-x2+1,故此函数有最大值为1,
当x>0时,y随x的增大而减小.
点评 此题主要考查了二次函数的定义以及二次函数的性质,正确掌握二次函数的性质是解题关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.
如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3秒时,△BPQ的面积为18cm2.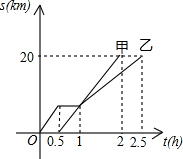 甲、乙从A出发,骑车沿同一条路行驶至B,他们离出发地的距离s(km)和时间t(h)间的函数图象如图所示,
甲、乙从A出发,骑车沿同一条路行驶至B,他们离出发地的距离s(km)和时间t(h)间的函数图象如图所示,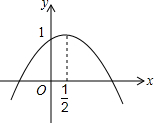 二次函数y=ax2+bx+c的图象如图所示.现有下列4个判断:①ac<0; ②a+b=0;③4ac-b2=4a;④a+b+c<0,其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示.现有下列4个判断:①ac<0; ②a+b=0;③4ac-b2=4a;④a+b+c<0,其中正确的有( ) 如图,⊙A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于3.
如图,⊙A中,弦DE=6,∠BAC+∠EAD=180°,则点A到弦BC的距离等于3.